Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Velká poloosa dráhy
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 2: | Řádka 2: | ||
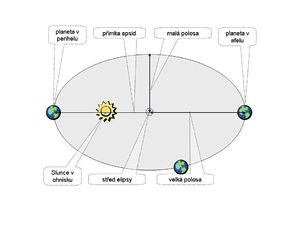
'''Velká poloosa dráhy''' je jedním z [[elementy dráhy|elementů dráhy]], popisujících pohyb [[kosmické těleso|kosmického tělesa]] (přirozeného, např. [[planeta|planety]], [[kometa|komety]] apod., nebo [[umělé kosmické těleso|umělého]]) v kosmickém prostoru. Značí se ''a'' a vyjadřuje se v délkových mírách; u přirozených kosmických těles, zejména planet ve [[Sluneční soustava|sluneční soustavě]] se používá nejčastěji [[astronomická jednotka|astronomické jednotky (AU)]]. Vyjadřuje střední vzdálenost kosmického tělesa od těžiště soustavy. | '''Velká poloosa dráhy''' je jedním z [[elementy dráhy|elementů dráhy]], popisujících pohyb [[kosmické těleso|kosmického tělesa]] (přirozeného, např. [[planeta|planety]], [[kometa|komety]] apod., nebo [[umělé kosmické těleso|umělého]]) v kosmickém prostoru. Značí se ''a'' a vyjadřuje se v délkových mírách; u přirozených kosmických těles, zejména planet ve [[Sluneční soustava|sluneční soustavě]] se používá nejčastěji [[astronomická jednotka|astronomické jednotky (AU)]]. Vyjadřuje střední vzdálenost kosmického tělesa od těžiště soustavy. | ||
U [[elipsa|eliptické dráhy]] je rovna [[aritmetický průměr|aritmetickému průměru]] hodnot vzdálenosti [[apsida (astronomie)|periapsidy (pericentra)]] a [[apsida (astronomie)|apoapsidy (apocentra)]] od těžiště soustavy, tedy | U [[elipsa|eliptické dráhy]] je rovna [[aritmetický průměr|aritmetickému průměru]] hodnot vzdálenosti [[apsida (astronomie)|periapsidy (pericentra)]] a [[apsida (astronomie)|apoapsidy (apocentra)]] od těžiště soustavy, tedy | ||
| - | :<big>\( a = \frac { R_P + R_A }{2}</ | + | :<big>\( a = \frac { R_P + R_A }{2}\)</big>, |
| - | kde <big>\(R_P</ | + | kde <big>\(R_P\)</big> je vzdálenost periapsidy a <big>\(R_A\)</big> je vzdálenost apoapsidy. |
Hodnota velké poloosy je přímo svázána s dalšími elementy dráhy podle [[Keplerovy zákony|3. Keplerova zákona]]. [[Doba oběhu|Doba oběhu (perioda)]] ''P'' je rovna | Hodnota velké poloosy je přímo svázána s dalšími elementy dráhy podle [[Keplerovy zákony|3. Keplerova zákona]]. [[Doba oběhu|Doba oběhu (perioda)]] ''P'' je rovna | ||
| - | :<big>\(P = 2 \pi \sqrt{ \frac { a^3 } { \mu } }</ | + | :<big>\(P = 2 \pi \sqrt{ \frac { a^3 } { \mu } }\)</big>, |
kde ''a'' je velká poloosa a ''μ'' je [[gravitační parametr]] [[centrální těleso|centrálního tělesa]]. | kde ''a'' je velká poloosa a ''μ'' je [[gravitační parametr]] [[centrální těleso|centrálního tělesa]]. | ||
Vyjádříme-li u těles pohybujících se Sluneční soustavou ''a'' v astronomických jednotkách, dostaneme pro dobu oběhu ''P'' v rocích zjednodušený výraz | Vyjádříme-li u těles pohybujících se Sluneční soustavou ''a'' v astronomických jednotkách, dostaneme pro dobu oběhu ''P'' v rocích zjednodušený výraz | ||
| - | :<big>\( P = \sqrt { a^3 }</ | + | :<big>\( P = \sqrt { a^3 }\)</big>. |
Pro [[střední denní pohyb]] resp. střední pohyb za jednotku času ''n'' vyjádřený ve [[obloukový stupeň|stupních]] za jednotku času | Pro [[střední denní pohyb]] resp. střední pohyb za jednotku času ''n'' vyjádřený ve [[obloukový stupeň|stupních]] za jednotku času | ||
| - | <big>\(n = \frac { 180 }{ \pi } \sqrt{ \frac { \mu } { a^3 } } </ | + | <big>\(n = \frac { 180 }{ \pi } \sqrt{ \frac { \mu } { a^3 } } \)</big>, |
kde ''a'' je velká poloosa a ''μ'' je [[gravitační parametr]] [[centrální těleso|centrálního tělesa]]. | kde ''a'' je velká poloosa a ''μ'' je [[gravitační parametr]] [[centrální těleso|centrálního tělesa]]. | ||
U [[hyperbola|hyperbolických drah]] je hodnota velké poloosy záporná (''a'' < 0). | U [[hyperbola|hyperbolických drah]] je hodnota velké poloosy záporná (''a'' < 0). | ||
U [[Parabola (matematika)|parabolické dráhy]] je hodnota velké poloosy nedefinovaná. Blíží-li se [[excentricita dráhy|excentricita]] eliptické dráhy k hodnotě 1 zleva (tj. elipsa se protahuje až se mění na parabolu), pak hodnota velké poloosy roste nade všechny meze, tj. | U [[Parabola (matematika)|parabolické dráhy]] je hodnota velké poloosy nedefinovaná. Blíží-li se [[excentricita dráhy|excentricita]] eliptické dráhy k hodnotě 1 zleva (tj. elipsa se protahuje až se mění na parabolu), pak hodnota velké poloosy roste nade všechny meze, tj. | ||
| - | :<big>\( \lim_{e \to 1} a = + \infty</ | + | :<big>\( \lim_{e \to 1} a = + \infty\)</big>. |
Naopak klesá-li u hyperbolické dráhy hodnota excentricity k hodnotě 1 zprava (tj. hyperbola se zužuje a mění se na parabolu), pak (záporná) hodnota velké poloosy klesá pode všechny meze, tj. | Naopak klesá-li u hyperbolické dráhy hodnota excentricity k hodnotě 1 zprava (tj. hyperbola se zužuje a mění se na parabolu), pak (záporná) hodnota velké poloosy klesá pode všechny meze, tj. | ||
| - | :<big>\( \lim_{e \to 1} a = - \infty</ | + | :<big>\( \lim_{e \to 1} a = - \infty\)</big>. |
== Související články == | == Související články == | ||
* [[Keplerovy zákony]] | * [[Keplerovy zákony]] | ||
Aktuální verze z 14. 8. 2022, 14:54
Velká poloosa dráhy je jedním z elementů dráhy, popisujících pohyb kosmického tělesa (přirozeného, např. planety, komety apod., nebo umělého) v kosmickém prostoru. Značí se a a vyjadřuje se v délkových mírách; u přirozených kosmických těles, zejména planet ve sluneční soustavě se používá nejčastěji astronomické jednotky (AU). Vyjadřuje střední vzdálenost kosmického tělesa od těžiště soustavy. U eliptické dráhy je rovna aritmetickému průměru hodnot vzdálenosti periapsidy (pericentra) a apoapsidy (apocentra) od těžiště soustavy, tedy
- \( a = \frac { R_P + R_A }{2}\),
kde \(R_P\) je vzdálenost periapsidy a \(R_A\) je vzdálenost apoapsidy. Hodnota velké poloosy je přímo svázána s dalšími elementy dráhy podle 3. Keplerova zákona. Doba oběhu (perioda) P je rovna
- \(P = 2 \pi \sqrt{ \frac { a^3 } { \mu } }\),
kde a je velká poloosa a μ je gravitační parametr centrálního tělesa. Vyjádříme-li u těles pohybujících se Sluneční soustavou a v astronomických jednotkách, dostaneme pro dobu oběhu P v rocích zjednodušený výraz
- \( P = \sqrt { a^3 }\).
Pro střední denní pohyb resp. střední pohyb za jednotku času n vyjádřený ve stupních za jednotku času \(n = \frac { 180 }{ \pi } \sqrt{ \frac { \mu } { a^3 } } \), kde a je velká poloosa a μ je gravitační parametr centrálního tělesa. U hyperbolických drah je hodnota velké poloosy záporná (a < 0). U parabolické dráhy je hodnota velké poloosy nedefinovaná. Blíží-li se excentricita eliptické dráhy k hodnotě 1 zleva (tj. elipsa se protahuje až se mění na parabolu), pak hodnota velké poloosy roste nade všechny meze, tj.
- \( \lim_{e \to 1} a = + \infty\).
Naopak klesá-li u hyperbolické dráhy hodnota excentricity k hodnotě 1 zprava (tj. hyperbola se zužuje a mění se na parabolu), pak (záporná) hodnota velké poloosy klesá pode všechny meze, tj.
- \( \lim_{e \to 1} a = - \infty\).
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |