V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.

Tečna kružnice

Z Multimediaexpo.cz

Broom icon.png Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte.
Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl. 		Broom icon.png
Tečna kružnice

Tečna kružnice je přímka, jež má s danou kružnicí právě jeden společný bod dotyku.

Obsah

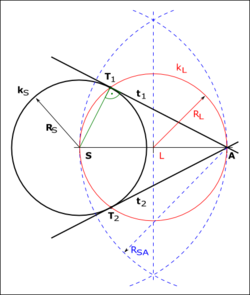
Narýsování tečny procházející bodem podle Thaletovy věty

Konstrukce tečny ke ružnici kS procházející daným bodem A.

Nechť je dána kružnice \(k_S</math> se středem \(S</math> a poloměrem \(R_S</math> a bod \(A</math> vně této kružnice. Ukážeme konstrukci tečny ke kružnici, která prochází bodem \(A</math>.

  1. Body \(S</math> a \(A</math> spojme přímkou.
  2. Zkonstruujme střed úsečky \(SA</math>, který označíme \(L</math>.
  3. Narýsujme kružnici \(k_L</math> se středem v bodě \(L</math> o poloměru \(R_L</math>, kde poloměr \(R_L</math> je roven velikosti úsečky \(LA</math> (a také \(LS</math>).
  4. V průniku kružnic \(k_S</math> a \(k_L</math> jsou body \(T_1</math> a \(T_2</math>
  5. Body \(T_1</math> a \(A</math> veďme přímku, která je tečnou \(t_1</math> ke kružnici \(k_S</math> v bodě \(T_1</math>
  6. Analogicky zkonstruujme tečnu \(t_2</math>.
  7. Thaleova věta říká, že úhel \(ST_1A</math> a \(ST_2A</math> je kolmý (90°), tedy je splněna podmínka tečny (jeden bod dotyku s kružnicí).

Narýsování tečny rovnoběžné s danou přímkou

Je dána kružnice \(k</math> se středem v bodě \(S</math> a přímka \(p</math>.

  1. Sestrojíme kolmici \(q</math> na přímku \(p</math> tak, aby procházela bodem \(S</math>
  2. Body, ve kterých se kružnice \(k</math> protne s přímkou \(q</math> označíme \(T</math> a \(T'</math>
  3. Sestrojíme dvě kolmice (tečny) na přímku \(q</math> procházející body \(T</math> a \(T'</math> a označíme je \(t</math> a \(t'</math>

Tečna v analytické geometrii

Tečna t ke kružnici k, se středem \(S\left[m;n \right]</math> a rovnicí:

\(\left( x - m \right)^2 + \left( y - n \right)^2=r^2</math>,

v bodě \(T_0\left[x_0;y_0 \right]</math> kružnice je zapsána rovnicí:

\(\left( x_0 - m \right)\left( x - m \right) + \left( y_0 - n \right)\left( y - n\right) =r^2</math>

Související články


Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/Te%C4%8Dna_kru%C5%BEnice“