V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Tečna kružnice
Z Multimediaexpo.cz
| Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl. |
|
Tečna kružnice je přímka, jež má s danou kružnicí právě jeden společný bod dotyku.
Obsah |
Narýsování tečny procházející bodem podle Thaletovy věty
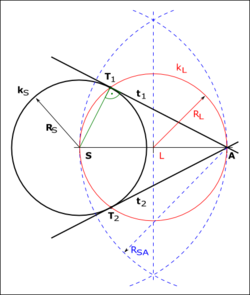
Nechť je dána kružnice \(k_S\) se středem \(S\) a poloměrem \(R_S\) a bod \(A\) vně této kružnice. Ukážeme konstrukci tečny ke kružnici, která prochází bodem \(A\).
- Body \(S\) a \(A\) spojme přímkou.
- Zkonstruujme střed úsečky \(SA\), který označíme \(L\).
- Narýsujme kružnici \(k_L\) se středem v bodě \(L\) o poloměru \(R_L\), kde poloměr \(R_L\) je roven velikosti úsečky \(LA\) (a také \(LS\)).
- V průniku kružnic \(k_S\) a \(k_L\) jsou body \(T_1\) a \(T_2\)
- Body \(T_1\) a \(A\) veďme přímku, která je tečnou \(t_1\) ke kružnici \(k_S\) v bodě \(T_1\)
- Analogicky zkonstruujme tečnu \(t_2\).
- Thaleova věta říká, že úhel \(ST_1A\) a \(ST_2A\) je kolmý (90°), tedy je splněna podmínka tečny (jeden bod dotyku s kružnicí).
Narýsování tečny rovnoběžné s danou přímkou
Je dána kružnice \(k\) se středem v bodě \(S\) a přímka \(p\).
- Sestrojíme kolmici \(q\) na přímku \(p\) tak, aby procházela bodem \(S\)
- Body, ve kterých se kružnice \(k\) protne s přímkou \(q\) označíme \(T\) a \(T'\)
- Sestrojíme dvě kolmice (tečny) na přímku \(q\) procházející body \(T\) a \(T'\) a označíme je \(t\) a \(t'\)
Tečna v analytické geometrii
Tečna t ke kružnici k, se středem \(S\left[m;n \right]\) a rovnicí:
- \(\left( x - m \right)^2 + \left( y - n \right)^2=r^2\),
v bodě \(T_0\left[x_0;y_0 \right]\) kružnice je zapsána rovnicí:
- \(\left( x_0 - m \right)\left( x - m \right) + \left( y_0 - n \right)\left( y - n\right) =r^2\)
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |