V encyklopedii Allmultimedia.cz byl aktivován špičkový grafický skin Foreground.
Foreground plně podporuje – RWD, HTML 5.0, Super Galerii a YouTube 2.0 !

Podobnost (geometrie)

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Aktualizace)
 
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Podobnost (geometrie)|700}}
+
[[Soubor:Similar-geometric-shapes.png|thumb|280px|Tvary se stejnou barvou jsou podobné]]
-
 
+
'''Podobnost''' je [[geometrické zobrazení]] Euklidovského prostoru do sebe, které násobí všechny vzdálenosti stejným koeficientem, tzv. měřítkem podobnosti. Dva geometrické útvary v [[Eukleidovský prostor|Euklidově prostoru]] jsou '''podobné''', pokud oba mají přesně stejný tvar. Přesněji řečeno, jeden je [[Shodné zobrazení|shodný]] s útvarem, získaným jako výsledek rovnoměrného zmenšení či zvětšení druhého a jeho případné [[Otočení|rotace]], [[posunutí (geometrie)|posunutí]] a [[Zrcadlení (matematika)|zrcadlení]]. Nejjednodušším příkladem podobného zobrazení je [[stejnolehlost]]. Podobnost je speciálním případem [[afinita|afinity]]. Speciálním případem podobnosti, je-li koeficient podobnosti roven 1, je [[shodné zobrazení|shodnost]].
 +
 
 +
Poměr vzdálenosti dvou bodů daného geometrického útvaru a vzdálenosti odpovídajících dvou bodů jiného geometrického útvaru (referenčního) je u podobných útvarů shodný ''pro každou takovou dvojici bodů'' a nazývá se '''koeficient podobnosti'''. Podobnost zachovává [[úhel#Velikost úhlu|velikost úhlů]] a [[poměr]] [[délka#Délka v geometrii|délek]].
 +
 
 +
== Podobnost v rovině ==
 +
Pro rovinné útvary z toho vyplývá, že odpovídající hrany podobných mnohoúhelníků jsou ve vzájemném poměru a odpovídající úhly si jsou rovny.
 +
 
 +
Například všechny [[kružnice]], [[Čtverec|čtverce]] a [[Rovnostranný trojúhelník|rovnostranné trojúhelníky]] si jsou podobné. Naopak [[Elipsa|elipsy]] si podobné být nemusí, stejně tak jako [[Hyperbola|hyperboly]].
 +
 
 +
Zpravidla se za speciální případ podobnosti považuje i shodnost, tedy podobnost s koeficientem podobnosti <big>\(k=1\)</big>. Všechny [[Shodné zobrazení|shodné]] tvary jsou tedy zároveň podobné (některé učebnice výslovně vydělují shodné trojúhelníky z definice podobných trojúhelníků, takže musí být rozdílné nejen tvary, ale i jejich velikosti, aby se daly považovat za podobné).<ref>Dvě kuželosečky jsou [[Podobnost (geometrie)|podobné]] právě tehdy, pokud mají stejnou [[Výstřednost kuželosečky|číselnou výstřednost]].</ref>
 +
 
 +
=== Podobné trojúhelníky ===
 +
Trojúhelníky <big>\(\triangle ABC\)</big> a <big>\(\triangle DEF\)</big> jsou podobné (píšeme <big>\(\triangle ABC\sim\triangle DEF \, \)</big>), pokud vyhoví jedné z následujících vět:
 +
 
 +
# ''Věta sss'' – Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících stran, jsou si podobné.
 +
#* odpovídající strany mají délky ve stejném poměru, takže platí <big>\( {AB \over DE} = {BC \over EF} = {AC \over DF} = k\)</big> a trojúhelníky jsou si podobné.
 +
# ''Věta sus'' – Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících stran a shodují se v úhlu jimi sevřeném, jsou si podobné.
 +
# ''Věta uu'' – Každé dva trojúhelníky, které mají dva úhly stejné, jsou si podobné.
 +
#* je-li úhel <big>\( \angle BAC\)</big> roven <big>\(\angle EDF\)</big> a <big>\(\angle ABC\)</big> je roven <big>\(\angle DEF\)</big>, pak to znamená, že i <big>\(\angle ACB\)</big> je roven <big>\(\angle DFE\)</big> a trojúhelníky jsou si podobné.
 +
# ''Věta Ssu'' – Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících stran a shodují se v úhlu naproti větší straně, jsou si podobné.
 +
Podobné trojúhelníky jsou tedy takové, které mají stejný tvar, ale jinou velikost (tvar trojúhelníku je definován jeho úhly). Je to možné říci i tak, že jeden trojúhelník je zvětšením (či zmenšením) druhého.
 +
 
 +
[[Soubor:SimilarRectangles.png|thumb|240px|Podobné obdélníky]]
 +
=== Podobné mnohoúhelníky ===
 +
Tuto myšlenku je možné rozšířit na [[mnohoúhelník]]y s více stranami. U jakýchkoli dvou podobných mnohoúhelníků si jsou odpovídající strany [[Přímá a nepřímá úměrnost|přímo úměrné]]. Nicméně pouze úměrnost stran není dostatečná k zajištění podobnosti mnohoúhelníků kromě trojúhelníků, takže odpovídající úhly rovněž musí být shodné.
 +
 
 +
== Související články ==
 +
* [[Geometrické zobrazení]]
 +
* [[Zobrazení (matematika)]]
 +
== Reference ==
 +
<references />
 +
== Externí odkazy ==
 +
 
 +
 
 +
{{Commonscat|Similarity (geometry)}}{{Článek z Wikipedie}}
[[Kategorie:Geometrie]]
[[Kategorie:Geometrie]]

Aktuální verze z 28. 7. 2025, 08:59

Tvary se stejnou barvou jsou podobné

Podobnost je geometrické zobrazení Euklidovského prostoru do sebe, které násobí všechny vzdálenosti stejným koeficientem, tzv. měřítkem podobnosti. Dva geometrické útvary v Euklidově prostoru jsou podobné, pokud oba mají přesně stejný tvar. Přesněji řečeno, jeden je shodný s útvarem, získaným jako výsledek rovnoměrného zmenšení či zvětšení druhého a jeho případné rotace, posunutí a zrcadlení. Nejjednodušším příkladem podobného zobrazení je stejnolehlost. Podobnost je speciálním případem afinity. Speciálním případem podobnosti, je-li koeficient podobnosti roven 1, je shodnost.

Poměr vzdálenosti dvou bodů daného geometrického útvaru a vzdálenosti odpovídajících dvou bodů jiného geometrického útvaru (referenčního) je u podobných útvarů shodný pro každou takovou dvojici bodů a nazývá se koeficient podobnosti. Podobnost zachovává velikost úhlů a poměr délek.

Obsah

Podobnost v rovině

Pro rovinné útvary z toho vyplývá, že odpovídající hrany podobných mnohoúhelníků jsou ve vzájemném poměru a odpovídající úhly si jsou rovny.

Například všechny kružnice, čtverce a rovnostranné trojúhelníky si jsou podobné. Naopak elipsy si podobné být nemusí, stejně tak jako hyperboly.

Zpravidla se za speciální případ podobnosti považuje i shodnost, tedy podobnost s koeficientem podobnosti \(k=1\). Všechny shodné tvary jsou tedy zároveň podobné (některé učebnice výslovně vydělují shodné trojúhelníky z definice podobných trojúhelníků, takže musí být rozdílné nejen tvary, ale i jejich velikosti, aby se daly považovat za podobné).[1]

Podobné trojúhelníky

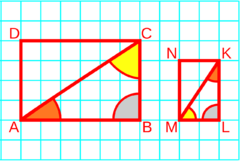
Trojúhelníky \(\triangle ABC\) a \(\triangle DEF\) jsou podobné (píšeme \(\triangle ABC\sim\triangle DEF \, \)), pokud vyhoví jedné z následujících vět:

  1. Věta sss – Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících stran, jsou si podobné.
    • odpovídající strany mají délky ve stejném poměru, takže platí \( {AB \over DE} = {BC \over EF} = {AC \over DF} = k\) a trojúhelníky jsou si podobné.
  2. Věta sus – Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících stran a shodují se v úhlu jimi sevřeném, jsou si podobné.
  3. Věta uu – Každé dva trojúhelníky, které mají dva úhly stejné, jsou si podobné.
    • je-li úhel \( \angle BAC\) roven \(\angle EDF\) a \(\angle ABC\) je roven \(\angle DEF\), pak to znamená, že i \(\angle ACB\) je roven \(\angle DFE\) a trojúhelníky jsou si podobné.
  4. Věta Ssu – Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících stran a shodují se v úhlu naproti větší straně, jsou si podobné.

Podobné trojúhelníky jsou tedy takové, které mají stejný tvar, ale jinou velikost (tvar trojúhelníku je definován jeho úhly). Je to možné říci i tak, že jeden trojúhelník je zvětšením (či zmenšením) druhého.

Podobné obdélníky

Podobné mnohoúhelníky

Tuto myšlenku je možné rozšířit na mnohoúhelníky s více stranami. U jakýchkoli dvou podobných mnohoúhelníků si jsou odpovídající strany přímo úměrné. Nicméně pouze úměrnost stran není dostatečná k zajištění podobnosti mnohoúhelníků kromě trojúhelníků, takže odpovídající úhly rovněž musí být shodné.

Související články

Reference

  1. ↑ Dvě kuželosečky jsou podobné právě tehdy, pokud mají stejnou číselnou výstřednost.

Externí odkazy

Commons nabízí fotografie, obrázky a videa k tématu
Podobnost (geometrie)
Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/Podobnost_(geometrie)“