Tečna kružnice
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Masivní vylepšení) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 5: | Řádka 5: | ||
== Narýsování tečny procházející bodem podle [[Thaletova věta|Thaletovy věty]] == | == Narýsování tečny procházející bodem podle [[Thaletova věta|Thaletovy věty]] == | ||
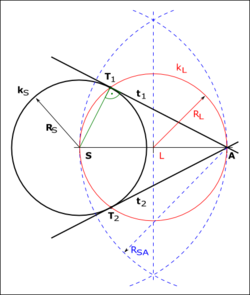
[[Soubor:CTVTP.png|thumb|250px|Konstrukce tečny ke ružnici '''k<sub>S</sub>''' procházející daným bodem '''A'''.]] | [[Soubor:CTVTP.png|thumb|250px|Konstrukce tečny ke ružnici '''k<sub>S</sub>''' procházející daným bodem '''A'''.]] | ||
| - | Nechť je dána kružnice '''< | + | Nechť je dána kružnice '''<big>\(k_S\)</big>''' se středem '''<big>\(S\)</big>''' a poloměrem '''<big>\(R_S\)</big>''' a bod '''<big>\(A\)</big>''' vně této kružnice. Ukážeme konstrukci tečny ke kružnici, která prochází bodem '''<big>\(A\)</big>'''. |
| - | # Body '''< | + | # Body '''<big>\(S\)</big>''' a '''<big>\(A\)</big>''' spojme přímkou. |
| - | # Zkonstruujme střed úsečky '''< | + | # Zkonstruujme střed úsečky '''<big>\(SA\)</big>''', který označíme '''<big>\(L\)</big>'''. |
| - | # Narýsujme kružnici '''< | + | # Narýsujme kružnici '''<big>\(k_L\)</big>''' se středem v bodě '''<big>\(L\)</big>''' o poloměru '''<big>\(R_L\)</big>''', kde poloměr '''<big>\(R_L\)</big>''' je roven velikosti úsečky '''<big>\(LA\)</big>''' (a také '''<big>\(LS\)</big>'''). |
| - | # V průniku kružnic '''< | + | # V průniku kružnic '''<big>\(k_S\)</big>''' a '''<big>\(k_L\)</big>''' jsou body '''<big>\(T_1\)</big>''' a '''<big>\(T_2\)</big>''' |
| - | # Body '''< | + | # Body '''<big>\(T_1\)</big>''' a '''<big>\(A\)</big>''' veďme přímku, která je tečnou '''<big>\(t_1\)</big>''' ke kružnici '''<big>\(k_S\)</big>''' v bodě '''<big>\(T_1\)</big>''' |
| - | # Analogicky zkonstruujme tečnu '''< | + | # Analogicky zkonstruujme tečnu '''<big>\(t_2\)</big>'''. |
| - | # Thaleova věta říká, že úhel '''< | + | # Thaleova věta říká, že úhel '''<big>\(ST_1A\)</big>''' a '''<big>\(ST_2A\)</big>''' je kolmý (90°), tedy je splněna podmínka tečny (jeden bod dotyku s kružnicí). |
== Narýsování tečny rovnoběžné s danou přímkou == | == Narýsování tečny rovnoběžné s danou přímkou == | ||
| - | Je dána kružnice '''< | + | Je dána kružnice '''<big>\(k\)</big>''' se středem v bodě '''<big>\(S\)</big>''' a [[přímka]] '''<big>\(p\)</big>'''. |
| - | # Sestrojíme kolmici '''< | + | # Sestrojíme kolmici '''<big>\(q\)</big>''' na přímku '''<big>\(p\)</big>''' tak, aby procházela bodem '''<big>\(S\)</big>''' |
| - | # Body, ve kterých se kružnice '''< | + | # Body, ve kterých se kružnice '''<big>\(k\)</big>''' protne s přímkou '''<big>\(q\)</big>''' označíme '''<big>\(T\)</big>''' a '''<big>\(T'\)</big>''' |
| - | # Sestrojíme dvě kolmice ('''tečny''') na přímku '''< | + | # Sestrojíme dvě kolmice ('''tečny''') na přímku '''<big>\(q\)</big>''' procházející body '''<big>\(T\)</big>''' a '''<big>\(T'\)</big>''' a označíme je '''<big>\(t\)</big>''' a '''<big>\(t'\)</big>''' |
== Tečna v analytické geometrii == | == Tečna v analytické geometrii == | ||
| - | Tečna ''t'' ke [[kružnice|kružnici]] ''k'', se středem < | + | Tečna ''t'' ke [[kružnice|kružnici]] ''k'', se středem <big>\(S\left[m;n \right]\)</big> a [[rovnice|rovnicí]]: |
| - | :< | + | :<big>\(\left( x - m \right)^2 + \left( y - n \right)^2=r^2\)</big>, |
| - | v bodě < | + | v bodě <big>\(T_0\left[x_0;y_0 \right]\)</big> kružnice je zapsána rovnicí: |
| - | :< | + | :<big>\(\left( x_0 - m \right)\left( x - m \right) + \left( y_0 - n \right)\left( y - n\right) =r^2\)</big> |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:53
Tečna kružnice je přímka, jež má s danou kružnicí právě jeden společný bod dotyku.
Obsah |
Narýsování tečny procházející bodem podle Thaletovy věty
Nechť je dána kružnice \(k_S\) se středem \(S\) a poloměrem \(R_S\) a bod \(A\) vně této kružnice. Ukážeme konstrukci tečny ke kružnici, která prochází bodem \(A\).
- Body \(S\) a \(A\) spojme přímkou.
- Zkonstruujme střed úsečky \(SA\), který označíme \(L\).
- Narýsujme kružnici \(k_L\) se středem v bodě \(L\) o poloměru \(R_L\), kde poloměr \(R_L\) je roven velikosti úsečky \(LA\) (a také \(LS\)).
- V průniku kružnic \(k_S\) a \(k_L\) jsou body \(T_1\) a \(T_2\)
- Body \(T_1\) a \(A\) veďme přímku, která je tečnou \(t_1\) ke kružnici \(k_S\) v bodě \(T_1\)
- Analogicky zkonstruujme tečnu \(t_2\).
- Thaleova věta říká, že úhel \(ST_1A\) a \(ST_2A\) je kolmý (90°), tedy je splněna podmínka tečny (jeden bod dotyku s kružnicí).
Narýsování tečny rovnoběžné s danou přímkou
Je dána kružnice \(k\) se středem v bodě \(S\) a přímka \(p\).
- Sestrojíme kolmici \(q\) na přímku \(p\) tak, aby procházela bodem \(S\)
- Body, ve kterých se kružnice \(k\) protne s přímkou \(q\) označíme \(T\) a \(T'\)
- Sestrojíme dvě kolmice (tečny) na přímku \(q\) procházející body \(T\) a \(T'\) a označíme je \(t\) a \(t'\)
Tečna v analytické geometrii
Tečna t ke kružnici k, se středem \(S\left[m;n \right]\) a rovnicí:
- \(\left( x - m \right)^2 + \left( y - n \right)^2=r^2\),
v bodě \(T_0\left[x_0;y_0 \right]\) kružnice je zapsána rovnicí:
- \(\left( x_0 - m \right)\left( x - m \right) + \left( y_0 - n \right)\left( y - n\right) =r^2\)
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |