V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.

Giniho koeficient

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (Nahrazení textu „<math>“ textem „<big>\(“)
m (Nahrazení textu „</math>“ textem „\)</big>“)
 
Řádka 6: Řádka 6:
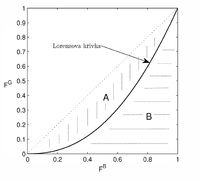
Giniho koeficient většinou definujeme jako poměr plochy mezi [[Lorenzova křivka|Lorenzovou křivkou]] a diagonálou jednotkového čtverce ('''A''') ku celkové ploše pod diagonálou ('''A+B'''), tedy  
Giniho koeficient většinou definujeme jako poměr plochy mezi [[Lorenzova křivka|Lorenzovou křivkou]] a diagonálou jednotkového čtverce ('''A''') ku celkové ploše pod diagonálou ('''A+B'''), tedy  
-
<big>\(GC=\frac{A}{A+B}.</math>
+
<big>\(GC=\frac{A}{A+B}.\)</big>
Protože obsah plochy pod diagonálou je polovina jednotkového čtverce, můžeme definici přepsat jako '''GC=2A''' nebo také '''GC=1-2B'''. Odtud použitím posledního jmenovaného výrazu dostáváme matematický vztah
Protože obsah plochy pod diagonálou je polovina jednotkového čtverce, můžeme definici přepsat jako '''GC=2A''' nebo také '''GC=1-2B'''. Odtud použitím posledního jmenovaného výrazu dostáváme matematický vztah
-
<big>\(GC= 1 - 2\int_S F^G(s) dF^B(s),</math>
+
<big>\(GC= 1 - 2\int_S F^G(s) dF^B(s),\)</big>
-
kde <big>\(F^G(s)</math> a <big>\(F^B(s)</math> jsou distribuční funkce dobrých a špatných klientů (viz [[skóringový model]]). Jiné vyjádření získáme, vyjdeme-li ze vztahu '''GC=2A'''. Potom
+
kde <big>\(F^G(s)\)</big> a <big>\(F^B(s)\)</big> jsou distribuční funkce dobrých a špatných klientů (viz [[skóringový model]]). Jiné vyjádření získáme, vyjdeme-li ze vztahu '''GC=2A'''. Potom
-
<big>\(GC= 2\int_S \big(F^B(s)-F^G(s)\big) dF^B(s).</math>
+
<big>\(GC= 2\int_S \big(F^B(s)-F^G(s)\big) dF^B(s).\)</big>
== Interpretace ==
== Interpretace ==
Řádka 23: Řádka 23:
Pro odhad Giniho koeficientu lze v praxi použít více postupů. Jedním z často používaných je odhad pomocí tzv. ''Somersovy d statistiky''.
Pro odhad Giniho koeficientu lze v praxi použít více postupů. Jedním z často používaných je odhad pomocí tzv. ''Somersovy d statistiky''.
-
Označíme-li <big>\(s_j</math> skóre j-tého klienta, můžeme definovat charakteristiky '''a''', '''b''' a '''c''' následovně:
+
Označíme-li <big>\(s_j\)</big> skóre j-tého klienta, můžeme definovat charakteristiky '''a''', '''b''' a '''c''' následovně:
-
* '''a''' je počet všech dvojic klientů (i,j), i>j takových, že rozdíly <big>\(s_i-s_j</math> a <big>\(y_i-y_j</math> jsou nenulové a mají stejné znaménko (tedy takových dvojic, kde dobrý klient byl ohodnocen větším skóre než špatný klient);
+
* '''a''' je počet všech dvojic klientů (i,j), i>j takových, že rozdíly <big>\(s_i-s_j\)</big> a <big>\(y_i-y_j\)</big> jsou nenulové a mají stejné znaménko (tedy takových dvojic, kde dobrý klient byl ohodnocen větším skóre než špatný klient);
-
* '''b''' je počet všech dvojic klientů (i,j), i>j takových, že rozdíly <big>\(s_i-s_j</math> a <big>\(y_i-y_j</math> jsou nenulové a mají opačné znaménko (tedy takových dvojic, kde dobrý klient byl ohodnocen menším skóre než špatný klient);
+
* '''b''' je počet všech dvojic klientů (i,j), i>j takových, že rozdíly <big>\(s_i-s_j\)</big> a <big>\(y_i-y_j\)</big> jsou nenulové a mají opačné znaménko (tedy takových dvojic, kde dobrý klient byl ohodnocen menším skóre než špatný klient);
-
* '''c''' je počet všech dvojic klientů (i,j), i>j takových, že <big>\(s_i=s_j</math> a <big>\(y_i\neq y_j</math> (tedy takových dvojic, kde dobrý klient byl ohodnocen stejným skóre jako špatný klient).
+
* '''c''' je počet všech dvojic klientů (i,j), i>j takových, že <big>\(s_i=s_j\)</big> a <big>\(y_i\neq y_j\)</big> (tedy takových dvojic, kde dobrý klient byl ohodnocen stejným skóre jako špatný klient).
Potom ''Somersovu d statistiku'' spočítáme jako
Potom ''Somersovu d statistiku'' spočítáme jako
-
<big>\(d = \frac{a-b}{a+b+c}.</math>
+
<big>\(d = \frac{a-b}{a+b+c}.\)</big>
== Související články ==
== Související články ==

Aktuální verze z 14. 8. 2022, 14:51

Země podle Giniho koeficientu. 0 znamená dokonalou rovnost příjmů. kde všichni mají stejný příjem, kdežto 1 znamená dokonalou nerovnost, kde jedna osoba má veškerý příjem a ostatní lidé nemají žádný.

Giniho koeficient je číselná charakteristika diverzifikace. Má veliké uplatnění v ekonomii, kde se jím poměřuje ekvivalence rozložení bohatství a důchodů v jednotlivých územních celcích, nejčastěji státech. Dále se často používá jako míra diverzifikační schopnosti skóringového modelu. Udává se od 0 do 1.

Obsah

Definice

Lorenzova křivka

Giniho koeficient většinou definujeme jako poměr plochy mezi Lorenzovou křivkou a diagonálou jednotkového čtverce (A) ku celkové ploše pod diagonálou (A+B), tedy

\(GC=\frac{A}{A+B}.\)

Protože obsah plochy pod diagonálou je polovina jednotkového čtverce, můžeme definici přepsat jako GC=2A nebo také GC=1-2B. Odtud použitím posledního jmenovaného výrazu dostáváme matematický vztah

\(GC= 1 - 2\int_S F^G(s) dF^B(s),\)

kde \(F^G(s)\) a \(F^B(s)\) jsou distribuční funkce dobrých a špatných klientů (viz skóringový model). Jiné vyjádření získáme, vyjdeme-li ze vztahu GC=2A. Potom

\(GC= 2\int_S \big(F^B(s)-F^G(s)\big) dF^B(s).\)

Interpretace

Giniho koeficient je tedy dvojnásobek plochy mezi Lorenzovou křivkou a diagonálou jednotkového čtverce, neboli ekvivalentně poměr této plochy a celkové plochy pod diagonálou. Hodnota Giniho koeficientu proto leží v intervalu [0,1], kde hodnota 0 značí perfektní (ideální) diverzifikační schopnost, hodnota 1 značí nulovou diverzifikační schopnost a záporné hodnoty značí opačnou klasifikaci skóringové funkce.

Somersovo d

Broom icon.png Tato část článku potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že jí vhodně vylepšíte.
Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl. 		Broom icon.png

Pro odhad Giniho koeficientu lze v praxi použít více postupů. Jedním z často používaných je odhad pomocí tzv. Somersovy d statistiky.

Označíme-li \(s_j\) skóre j-tého klienta, můžeme definovat charakteristiky a, b a c následovně:

  • a je počet všech dvojic klientů (i,j), i>j takových, že rozdíly \(s_i-s_j\) a \(y_i-y_j\) jsou nenulové a mají stejné znaménko (tedy takových dvojic, kde dobrý klient byl ohodnocen větším skóre než špatný klient);
  • b je počet všech dvojic klientů (i,j), i>j takových, že rozdíly \(s_i-s_j\) a \(y_i-y_j\) jsou nenulové a mají opačné znaménko (tedy takových dvojic, kde dobrý klient byl ohodnocen menším skóre než špatný klient);
  • c je počet všech dvojic klientů (i,j), i>j takových, že \(s_i=s_j\) a \(y_i\neq y_j\) (tedy takových dvojic, kde dobrý klient byl ohodnocen stejným skóre jako špatný klient).

Potom Somersovu d statistiku spočítáme jako

\(d = \frac{a-b}{a+b+c}.\)

Související články

Externí odkazy


Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/Giniho_koeficient“