Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Deltoid
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 18: | Řádka 18: | ||
[[Obsah]] deltoidu je roven | [[Obsah]] deltoidu je roven | ||
| - | :<big>\(S = {1\over 2} e f</ | + | :<big>\(S = {1\over 2} e f\)</big>, |
| - | kde <big>\(e, f</ | + | kde <big>\(e, f\)</big> jsou délky jeho úhlopříček. |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:51
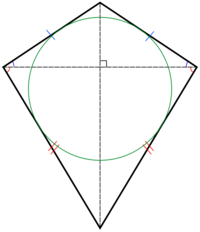
Deltoid je konvexní čtyřúhelník osově souměrný podle právě jedné úhlopříčky. Ta se nazývá hlavní úhlopříčka a druhá vedlejší úhlopříčka.
Má tvar (klasického létajícího) draka a ryze anglický termín pro deltoid je "kite" (drak) a ryze německý výraz je "Drachenviereck" (dračí čtyřúhelník).
Vlastnosti
Z osové souměrnosti deltoidu plyne, že jeho úhlopříčky jsou navzájem kolmé, strany vycházející ze stejných vrcholů na hlavní úhlopříčce mají stejnou délku a vedlejší úhlopříčka ose je hlavní úhlopříčkou půlena.
Hlavní úhlopříčka dělí deltoid na dva shodné trojúhelníky a vedlejší na dva rovnoramenné trojúhelníky, mající tvar řeckého písmene delta, odtud název.
Deltoid je určen (až na shodnost) třemi prvky, z nichž aspoň jeden musí mít rozměr délky.
Deltoidu lze vždy vepsat kružnici, je to tečnový čtyřúhelník.
Deltoid je zároveň tětivový čtyřúhelník, právě když úhly u vrcholů vedlejší úhlopříčky jsou pravé, potom je to dvojstředový čtyřúhelník. Ten je určen dvěma prvky, z nichž aspoň jeden musí mít rozměr délky. Jeho tvar je určen např. jedním úhlem při vrcholu hlavní úhlopříčky nebo poměrem stran při vrcholu vedlejší úhlopříčky.
Deltoid je různoběžník – žádné dvě strany nejsou rovnoběžné.
Obsah deltoidu je roven
- \(S = {1\over 2} e f\),
kde \(e, f\) jsou délky jeho úhlopříček.
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |