V encyklopedii Allmultimedia.cz byl aktivován špičkový grafický skin Foreground.
Foreground plně podporuje – RWD, HTML 5.0, Super Galerii a YouTube 2.0 !

Newtonova interpolace

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Aktualizace)
 
(Není zobrazena jedna mezilehlá verze.)
Řádka 1: Řádka 1:
-
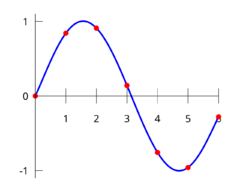
{{Wikipedia-cs|Newtonova interpolace|700}}
+
[[Soubor:Interpolation example polynomial.png|thumb|240px|Příklad interpolace polynomem – interpolační funkce vždy prochází všemi známými body funkce]]
 +
Chceme-li aproximovat [[Funkce (matematika)|funkci]] danou svými body <big>\( x_0 \cdots x_n \)</big> (tzv. uzly interpolace), a požadujeme aby [[interpolace]] '''procházela''' zadanými body, použijeme [[aproximace|aproximaci]] interpolačním [[polynom]]em.
 +
Tato interpolace nám poslouží k získání přibližné hodnoty funkce v libovolném bodě intervalu <big>\(<x_0,x_n>\)</big>.
 +
 +
; Tvar Newtonova interpolačního polynomu:
 +
 +
<big>\(N_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0)(x-x_1)+...+a_n(x-x_0)(x-x_1)...(x-x_{n-1})\)</big>
 +
 +
Koeficienty <big>\(a_0 \cdots a_n\)</big> lze vypočítat pomocí '''poměrných diferencí'''. (viz níže)
 +
 +
== Sestavení tabulky poměrných diferencí ==
 +
V každém sloupci tabulky se budou nacházet poměrné diference daného řádu. Diferencemi 0. řádu budou přímo funkční hodnoty v bodech <big>\(x_i\)</big>.
 +
 +
; Poměrné diference 1. řádu vyjádříme:
 +
 +
<big>\(f[x_i,x_{i+1}] = \frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}\)</big>
 +
 +
; Poměrné diference 2. řádu vyjádříme:
 +
 +
<big>\(f[x_i,x_{i+1},x_{i+2}] = \frac{f[x_{i+1},x_{i+2}]-f[x_i,x_{i+1}]}{x_{i+2}-x_i}\)</big>
 +
 +
Ostatní diference vyjádříme analogicky.
 +
 +
== Příklad konstrukce Newtonova interpolačního polynomu ==
 +
{{RIGHTTOC}}
 +
Hledáme polynom procházející body: <big>\([-2,-39], [0,3], [1,6], [3,36]\)</big>
 +
 +
{|class="wikitable"
 +
! <big>\(x_i\)</big> !! <big>\(f(x_i)\)</big> !! Diference 1. řádu !! Diference 2. řádu !! Diference 3. řádu
 +
|-
 +
| <big>\(x_0=-2\)</big>&nbsp;&nbsp; || <big>\(f(x_0)=-39=a_0\)</big>&nbsp;&nbsp; ||  ||  ||
 +
|-
 +
| <big>\(x_1=0\)</big> || <big>\(f(x_1)=3\)</big> || <big>\(\frac{3-(-39)}{0-(-2)}=21=a_1\)</big> ||  ||
 +
|-
 +
| <big>\(x_2=1\)</big> || <big>\(f(x_2)=6\)</big> || <big>\(\frac{6-3}{1-0}=3\)</big> || <big>\(\frac{3-21}{1-(-2)}=-6=a_2\)</big> ||
 +
|-
 +
| <big>\(x_3=3\)</big> || <big>\(f(x_3)=36\)</big> || <big>\(\frac{36-6}{3-1}=15\)</big> || <big>\(\frac{15-3}{3-0}=4\)</big> || <big>\(\frac{4-(-6)}{3-(-2)}=2=a_3\)</big>
 +
|}
 +
 +
<big>\(P_3(x) = a_0 + a_1(x-x_0) + a_2(x-x_0)(x-x_1) + a_3(x-x_0)(x-x_1)(x-x_2)\)</big>
 +
 +
<big>\(P_3(x) = -39 +21(x+2) -6(x+2)x +2(x+2)x(x-1) \)</big>
 +
 +
== Vlastnosti interpolační metody ==
 +
Newtonův interpolační polynom má tu výhodu, že je pro něj oproti [[Lagrangeova interpolace|Lagrangeově interpolaci]] výpočetně méně náročné přidat jeden bod, protože některé výpočty zůstanou beze změny (například předchozí koeficienty <big>\(a_k\)</big> se nezmění).
 +
 +
== Související články ==
 +
* [[Lagrangeova interpolace]]
 +
* [[Metoda nejmenších čtverců]]
 +
* [[Geometrie]] – více informací o křivkách
 +
 +
== Externí odkazy ==
 +
* [http://kfe.fjfi.cvut.cz/~limpouch/numet/aprox/node5.html Jiří Limpouch – Newtonův interpolační polynom]
 +
 +
 +
{{Článek z Wikipedie}}
[[Kategorie:Geometrie]]
[[Kategorie:Geometrie]]

Aktuální verze z 27. 7. 2025, 22:25

Příklad interpolace polynomem – interpolační funkce vždy prochází všemi známými body funkce

Chceme-li aproximovat funkci danou svými body \( x_0 \cdots x_n \) (tzv. uzly interpolace), a požadujeme aby interpolace procházela zadanými body, použijeme aproximaci interpolačním polynomem.

Tato interpolace nám poslouží k získání přibližné hodnoty funkce v libovolném bodě intervalu \(<x_0,x_n>\).

Tvar Newtonova interpolačního polynomu

\(N_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0)(x-x_1)+...+a_n(x-x_0)(x-x_1)...(x-x_{n-1})\)

Koeficienty \(a_0 \cdots a_n\) lze vypočítat pomocí poměrných diferencí. (viz níže)

Sestavení tabulky poměrných diferencí

V každém sloupci tabulky se budou nacházet poměrné diference daného řádu. Diferencemi 0. řádu budou přímo funkční hodnoty v bodech \(x_i\).

Poměrné diference 1. řádu vyjádříme

\(f[x_i,x_{i+1}] = \frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}\)

Poměrné diference 2. řádu vyjádříme

\(f[x_i,x_{i+1},x_{i+2}] = \frac{f[x_{i+1},x_{i+2}]-f[x_i,x_{i+1}]}{x_{i+2}-x_i}\)

Ostatní diference vyjádříme analogicky.

Příklad konstrukce Newtonova interpolačního polynomu

Hledáme polynom procházející body: \([-2,-39], [0,3], [1,6], [3,36]\)

\(x_i\) \(f(x_i)\) Diference 1. řádu Diference 2. řádu Diference 3. řádu
\(x_0=-2\)   \(f(x_0)=-39=a_0\)  
\(x_1=0\) \(f(x_1)=3\) \(\frac{3-(-39)}{0-(-2)}=21=a_1\)
\(x_2=1\) \(f(x_2)=6\) \(\frac{6-3}{1-0}=3\) \(\frac{3-21}{1-(-2)}=-6=a_2\)
\(x_3=3\) \(f(x_3)=36\) \(\frac{36-6}{3-1}=15\) \(\frac{15-3}{3-0}=4\) \(\frac{4-(-6)}{3-(-2)}=2=a_3\)

\(P_3(x) = a_0 + a_1(x-x_0) + a_2(x-x_0)(x-x_1) + a_3(x-x_0)(x-x_1)(x-x_2)\)

\(P_3(x) = -39 +21(x+2) -6(x+2)x +2(x+2)x(x-1) \)

Vlastnosti interpolační metody

Newtonův interpolační polynom má tu výhodu, že je pro něj oproti Lagrangeově interpolaci výpočetně méně náročné přidat jeden bod, protože některé výpočty zůstanou beze změny (například předchozí koeficienty \(a_k\) se nezmění).

Související články

Externí odkazy


Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/Newtonova_interpolace“