Kruhová výseč

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)

Kruhová výseč – zelená plocha

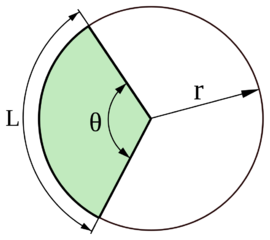
Kruhová výseč je část kruhu příslušná určitému středovému úhlu θ.

Obsah kruhu se rovná \(\pi r^2\,\!\)

Obsah výseče příslušné středovému úhlu 1° je roven \(\frac{1}{360}\) obsahu kruhu, tedy \(\frac{\pi r^2}{360}\)

Obsah výseče příslušné úhlu θ (zadaného v radiánech) je roven \( S = \frac{\theta r^2}{2} \).

Obvod celé výseče je roven součtu délky kruhového oblouku a dvojnásobku poloměru, tedy \(o = (\theta + 2) r\,\!\).
Úhel θ je zadán v radiánech.

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii

@@ Řádka 5: / Řádka 5: @@
 == Obsah výseče ==
-[[Obsah]] [[Kružnice|kruhu]] se rovná <math>\pi r^2\,\!</math>
+[[Obsah]] [[Kružnice|kruhu]] se rovná <big>\(\pi r^2\,\!\)</big>
-Obsah výseče příslušné středovému úhlu 1° je roven <math>\frac{1}{360}</math> obsahu [[Kruh (geometrie)|kruhu]], tedy <math>\frac{\pi r^2}{360}</math>
+Obsah výseče příslušné středovému úhlu 1° je roven <big>\(\frac{1}{360}\)</big> obsahu [[Kruh (geometrie)|kruhu]], tedy <big>\(\frac{\pi r^2}{360}\)</big>
-Obsah výseče příslušné úhlu θ (zadaného v [[radián]]ech) je roven <math> S = \frac{\theta r^2}{2} </math>.
+Obsah výseče příslušné úhlu θ (zadaného v [[radián]]ech) je roven <big>\( S = \frac{\theta r^2}{2} \)</big>.
 == Obvod výseče ==
-* [[Obvod (geometrie)|Obvod]] celé výseče je roven součtu délky [[kruhový oblouk|kruhového oblouku]] a dvojnásobku [[poloměr]]u, tedy <math>o = (\theta + 2) r\,\!</math>.
+* [[Obvod (geometrie)|Obvod]] celé výseče je roven součtu délky [[kruhový oblouk|kruhového oblouku]] a dvojnásobku [[poloměr]]u, tedy <big>\(o = (\theta + 2) r\,\!\)</big>.
 * Úhel θ je zadán v [[radián]]ech.