Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Matematický koprocesor
Z Multimediaexpo.cz
Matematický koprocesor případně numerický koprocesor, někdy zkráceně jen koprocesor (angl. numeric coprocessor, math coprocessor zkráceně MCP nebo floating-point unit zkráceně FPU) je koprocesor určený na vykonávání operácí s čísly s plovoucí desetinnou čárkou. Některé typy matematických koprocesorů jsou schopné vykonávání i složitějších matematických operácí. Matematický koprocesor může být implementovaný jako samostatná jednotka nebo může být součástí CPU.
V minulosti procesory neobsahovaly žádný zabudovaný mechanizmus na zpracování čísel s plovoucí desetinnou čárkou. Zpracování těchto čísel bylo realizované externím matematickým koprocesorem případně bylo emulované mikroprogramem v aritmeticko-logické jednotce procesoru. Vykonávání operácí s čísly s pohyblivou desetinnou čárkou emulací v ALJ je však mnohem pomalejší a navíc zatěžuje hlavní procesor.
Přestože je možné softwarovou emulací matematického koprocesoru ušetřit výrobní náklady, v současných procesorech pro osobní počítače je matematický koprocesor integrovaný v mikroprocesoru. To bylo umožněno prudkým poklesem výrobních nákladů v posledních letech.
Obsah |
Koprocesory Intel 8087
Koprocesor Intel 8087 byl přídavný matematický koprocesor dodávaný pro procesory Intel 8086, doplňující jejich funkčnost o podporu práce s reálnými čísly (přesněji s čísly s pohyblivou řádovou čárkou). Byl poměrně drahý, dal se však softwarově emulovat (což bylo asi desetkrát pomalejší).
Z matematického koprocesoru Intel 8087 vycházely i koprocesory pro novější procesory Intel: koprocesory 80287 (pro procesor 80286), 80387 (pro procesor 80386) a 80487 (???; pro procesor 80486 SX). Procesory 80486 DX a následující (Pentium) měly již matematický koprocesor integrovaný v sobě – v těchto případech již pojem matematický koprocesor v podstatě ztrácí smysl a je lepší používat pojem FPU.
Vnitřní struktura FPU
FPU je jednotka pro práci s čísly s pohyblivou řádovou čárkou (jak je patrno již jejícho názvu – Floating Point Unit). Z pohledu programátora obsahuje následující registry:
- osm registrů po 80 bitech pro ukládání čísel s pohyblivou řádovou čárkou. Tyto registry se označují jako ST0 až ST7 a chovají se jako zásobník s vrcholem ST0. Lze však i přistupovat k libovolnému ST registru přímo.
- registr známek (Tag register) – šestnáctibitový registr uchovávající informace o jednotlivých ST registrech (každému ST registru jsou přiřazeny dva bity pro uchování jedné ze čtyř hodnot: zda je prázdný, obsahuje platné číslo, nulu nebo neplatné číslo)
- stavový a řídící registr (Status register a Control (word) register) – šestnáctibitové registry funkčně zhruba odpovídající registru Flags procesorů 80x86
Jednotka FPU pracuje se třemi formáty čísel s pohyblivou řádovou čárkou:
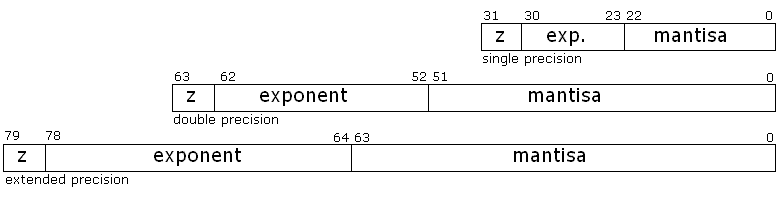
- single precision (32 bitů) – podle standardu IEEE
- double precision (64 bitů) – podle standardu IEEE
- extended precision (80 bitů) nestandardní formát Intelu
Tyto formáty se v podstatě liší jen datovou velikostí – samotné číslo je v nich ukládáno stejným způsobem: znaménko (1 bit) – exponent – mantisa
Znaménko je vždy ukládáno na nejvyšším bitu. Nula značí plus, jednička mínus
Exponent je ukládán na osmi bitech (u single precision) nebo na 11 bitech (u double precision). Je ukládán v kódu transformované nuly (též aditivní kód – viz Dvojková soustava).
Mantisa je ukádána na „zbytku“ bitů, tj. na 23 (single precision) resp. 52 (double precision) bitech. Její tvar závisí na typu uloženého čísla (viz dále).
Typy čísel uložitelných v STx registrech
V STx registrech lze ukádat čísla jak IEEE formátech (single a double precision), tak čísla v 80bitovém formátu Intel.
Ve všech těchto třech formátech lze ukládat následující typy čísel:
- normalizovaná čísla – čísla ve tvaru +/− 1.mmmm… · 2eeee…. Tato čísla jsou reprezentována jakoukoli hodnotou uloženou v mantise a jakoukoli hodnotou v exponentu s výjimkou nuly a nejvyšší uložitelné hodnoty. Mantisa začíná vždy jedničkou následovanou desetinnou čárkou; povšimněte si, že je uložena s vynecháním jedničky na začátku, např. mantisa 1.01100110 je uložena jako 01100110.
- denormalizovaná čísla – jsou reprezentována nulovým exponentem a libovolnou nenulovou hodnotou uloženou v mantise. Mantisa je uložena s pevnou řádovou čárkou ve tvaru m.mmmm…, tj. mantisa 0.0011001 je uložena jako 00011001. Tato čísla se využívají pro ukládání velmi malých hodnot, která nejdou uložit normalizovaně.
- nula – je reprezentována nulovým exponentem a nulovou mantisou
- nekonečno (infinity) – je reprezentováno maximálním exponentem a nulovou mantisou. Toto číslo vznikne např. po dělení nulou.
- nečíselná hodnota (NaN, Not a Number) – je reprezentována maximálním exponentem a nenulovou mantisou, toto „číslo“ vznikne např. po dělení 0/0.
Tabulka uložitelných hodnot pro single precision (pro ostatní formáty bude tabulka obdobná)
| typ čísla | exponent | mantisa v paměti | význam paměťové mantisy | odpovídající známka (v Tag registru) |
|---|---|---|---|---|
| normalizované číslo | 0 < exponent < 255 | m = libovolná hodnota | desetinná část skutečné mantisy (tvar 1,mmmm) | 0 |
| denormalizované číslo | 0 | libovolná nenulová hodnota | skutečná mantisa s pevnou desetinnou čárkou za nejvyšším bitem | 2 |
| nula | 0 | 0 | 0 | 1 |
| nekonečno | 255 | 0 | — | 2 |
| nečíselná hodnota | 255 | libolná nenulová hodnota | — | 2 |
Související články
Externí odkazy
- IEEE-754 References (anglicky)
- ANSI/IEEE 854 – History and Minutes (anglicky)
- Floating Point Unit by Jidan Al-Eryani (PDF, anglicky)
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |