V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
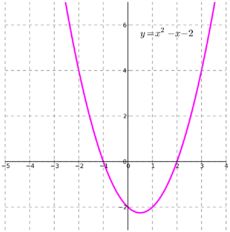
Kvadratická funkce
Z Multimediaexpo.cz
Kvadratická funkce je taková funkce, jejíž hodnota se mění úměrně druhé mocnině nezávislé proměnné.
Například funkce <math>y = -2x^2 + 5x + {1 \over 2}</math> je kvadratická.
Ryze kvadratická funkce je pak funkce bez lineárního členu x, například <math>y = 3x^2 - 10</math>.
Definice
Funkce f je kvadratická, pokud ji lze vyjádřit ve tvaru <math>f(x) = a \cdot x^2 + b \cdot x + c</math>,
kde a, b i c jsou konstanty a <math>a \ne 0</math>.
Definiční obor kvadratické funkce je <math>( - \infty, \infty )</math>.
Vlastnosti
- grafem kvadratické funkce je parabola
- kvadratická funkce má v každém bodě derivaci
- příklad: funkce <math>f(x) = 5x^2 + 3x - 6</math> má derivaci <math>f'(x) = 10x + 3</math>
- primitivní funkce ke kvadratické funkci je funkce kubická
- příklad: <math>\int 5x^2 + 3x - 6 \, dx = {5 \over 3} x^3 + {3 \over 2}x^2 - 6x + C</math>
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |