Naše návštěvnost dne 25. února 2026 byla — 484 927 unikátních návštěvníků !!
Logistická funkce
Z Multimediaexpo.cz
Logistická funkce nebo též logistická křivka je reálná funkce definovaná jako
- \(f(t;a,m,n,\tau) = a\frac{1 + m e^{-t/\tau}}{1 + n e^{-t/\tau}} \!\)
kde f je funkční hodnota, a, m, n, a τ reálné parametry. Nezávisle proměnnou označujeme jako t, protože logistická funkce se často používá pro modelování vývoje v čase. V počáteční fázi je růst přibližně exponenciální, později s rostoucím nasycením se zpomaluje, a nakonec se asymptoticky zastaví. Logistická funkce se často používá v empirických vědách pro modelování růstu populací, koncentrací a podobně.
Sigmoida
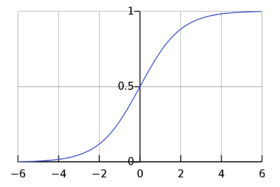
Významným příkladem logistické funkce je speciální případ s parametry a = 1, m = 0, n = 1, τ = 1, tedy
- \(P(t) = \frac{1}{1 + e^{-t}}\!\)
Tato logistická funkce se pro svůj tvar někdy označuje též jako sigmoida. Je řešením nelineární diferenciální rovnice prvního řádu
- \(\frac{\mathrm{d}P}{\mathrm{d}t}=P(1-P), \quad\mbox{(2)}\!\)
s okrajovou podmínkou P(0) = 1/2. Používá se často jako sponová funkce (link function) ve statistických modelech (logistická regrese).
Význam
Logistické křivky se objevují jako řešení různých modelů například v demografii, biologii a ekonomii.
Související články
- Gaussova křivka (distribuční funkce normálního rozdělení)
- Hyperbolický tangens
- Chybová funkce
- Logistická regrese
- Přechodové jevy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |