V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.

Křivka

Z Multimediaexpo.cz

Verze z 14. 8. 2022, 14:52; Sysop (diskuse | příspěvky)
(rozdíl) ← Starší verze | zobrazit aktuální verzi (rozdíl) | Novější verze → (rozdíl)


Křivka je v matematice geometrický jednorozměrný objekt, případně zobrazení z úsečky do nějakého matematického prostoru (tzv. parametrizovaná křivka). Jednoduchý příklad křivky je například kružnice nebo přímka.

Obsah

Formální definice

Je-li M nějaký matematický prostor (například Eukleidovský prostor, varieta, topologický prostor) a I interval reálných čísel, pak křivkou \(k\) rozumíme spojité zobrazení z I do M. Toto se někdy také nazývá parametrická křivka. Pokud má smysl mluvit o derivaci k (t.j. pokud cílový prostor je Euklidův prostor nebo hladká varieta a derivace existuje v každém bodě), nazývá se křivka hladká, anebo diferenciální. Hladká křivka je regulární, pokud její derivace není v žádném bodě nulová. Křivka se nazývá uzavřená, pokud I je uzavřený interval [a,b] a \(k(a)=k(b)\). Množina \(\{k(x);\,x\in I\}\) se nazývá obraz křivky. Mají-li složky \(k_i\) křivky k na otevřeném intervalu \((a,b)\) spojité derivace až do \(r\)-tého řádu, pak říkáme, že se jedná o křivku \(r\)-té třídy. Má-li křivka všechny derivace, říkáme někdy, že je třídy nekonečno, nebo-li někonečně diferencovatelná. Někdy se slovem křivka myslí jenom obraz křivky (v dřívější definici), t.j. množina bodů. Toto se někdy také nazývá neparametrická křivka.

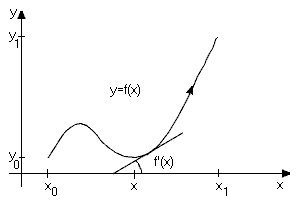
Rovinná křivka

Rovinnou křivkou rozumíme zobrazení

\(x = \phi(t)\)
\(y = \psi(t)\)

pro \(t \in \langle\alpha,\beta\rangle\), kde \(\phi\) a \(\psi\) jsou spojité funkce. Předpokládáme obvykle, že funkce \(\phi(t), \psi(t)\) jsou na intervalu \(\langle\alpha,\beta\rangle\) spojité a mají na tomto intervalu po částech spojité derivace \(\phi^\prime(t), \psi^\prime(t)\). Někdy se předpokládá, že funkce \(\phi, \psi\) jsou pouze spojité, pak se ale může stát že obraz křivky je celý dvourozměrný čtverec. Křivku nazveme regulární, pokud pro žádné \(t\) nejsou derivace \(\phi^\prime(t), \psi^\prime(t)\) současně nulové. Křivku, která neprotíná sama sebe (t.j. je prostá) označujeme jako jednoduchou. Rovnici obrazu rovinné křivky lze často vyjádřit ve formě funkční závislosti proměnných \(x, y\), tzn.

\(y=f(x)\),

popř.

\(F(x,y)=0\).

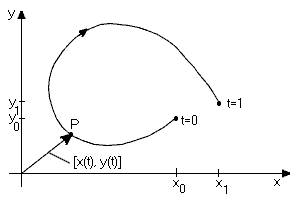
Pokud platí současně \(\phi(\alpha)=\phi(\beta), \psi(\alpha)=\psi(\beta)\), tzn. počáteční bod křivky splývá s bodem koncovým, pak křivku označíme jako uzavřenou. Křivku označíme jako rektifikovatelnou, pokud má konečnou délku, kterou lze vyjádřit jako

\(l = \int_\alpha^\beta \sqrt{{\phi^\prime}^2(t)+{\psi^\prime}^2(t)}\mathrm{d}t\)

Někdy se také slovem křivka myslí množina bodů \(\{(\phi(t), \psi(t));\, t\in<\alpha,\beta>\}\).

Jordanova křivka

Jednoduchou rektifikovatelnou uzavřenou křivku (která nemusí být po částech hladká) označujeme jako Jordanovu křivku. Jordanova křivka je uzavřená, takže rozděluje rovinu na dvě souvislé oblasti. Tu, která je omezená označujeme jako vnitřek křivky (nebo Jordanovu oblast), zbytek roviny pak jako vnějšek křivky.

Orientace křivky

Na neparametrické hladké křivce (t.j. množině, která je obrazem parametrické hladké křivky) můžme zvolit dvě orientace, což je volba směru, kterým se křivka pohybuje. Formálněji, je to volba baze jejího (jednorozměrného) tečného prostoru v každém bodě. Tvoří-li uzavřená křivka hranici určité oblasti \(\Omega\), pak řekneme, že je kladně orientovaná vzhledem k \(\Omega\), pokud oblast \(\Omega\) zůstává po levé straně křivky (při pohybu po kladně orientované křivce jde o pohyb proti směru hodinových ručiček). Formálněji, křivka je kladně orientována, pokud normálový vektor k oblasti \(\Omega\) a tečný vektor ke křivce určen její orientací tvoří kladnou bázi tečného prostoru (souřadnice těchto vektorů napsány ve sloupcích vedle sebe tvoří matici, která má kladný determinant). V opačném případě se jedná o záporně orientovanou křivku.

Příklady rovinných křivek

Prostorová křivka

Prostorovou křivkou rozumíme zobrazení

\(x = x(t)\)
\(y = y(t)\)
\(z = z(t)\)

pro \(t \in \langle\alpha,\beta\rangle\), kde x, y a z jsou spojité funkce. Uvedené rovnice křivky bývají obvykle zapisovány ve vektorovém tvaru

\(\mathbf{r} = \mathbf{r}(t)\),

kde \(\mathbf{r}\) představuje rádiusvektor. Křivku v prostoru lze také zadat jako průnik dvou ploch, např.

\(z=f(x,y)\)
\(z=g(x,y)\)

nebo

\(F(x,y,z)=0\)
\(G(x,y,z)=0.\)

Jsou-li rovnice popisující křivku algebraické, pak křivku označujeme jako algebraickou. Pokud uvedené rovnice nejsou algebraické, pak říkáme, že křivka je transcendentní. Někdy se také slovem křivka myslí množina bodů \(\{(x(t), y(t), z(t));\, t\in<\alpha,\beta>\}\).

Příklady prostorových křivek

Oblouk křivky

Obloukem křivky \(k: [a,b]\to \R^n\) od bodu \(t_0 \in \langle a,b\rangle\) do bodu \(t \in \langle a,b\rangle\) se nazývá délka části křivky mezi k(t_0) a k(t). Pokud je křivka diferencovatelná (t.j. k má derivace), dá se spočíst vzorcem

\(s = \int_{t_0}^t \sqrt{{\sum_i \left(\frac{\mathrm{d}k_i}{\mathrm{d}t}\right)}^2} \mathrm{d} t\)

kde \(k_i\) je i-tá složka křivky. Diferenciál

\(\mathrm{d}s = \sqrt{\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}\cdot\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}}\mathrm{d}t = \sqrt{\mathrm{d}\mathbf{r}\cdot\mathrm{d}\mathbf{r}} = \sqrt{\sum_i\mathrm{d}k_i^2}\)

nazýváme diferenciál (prvek, element) oblouku nebo lineární prvek (element) křivky.

Křivky vyplňující prostor

Obrazem křivky můžou být i množiny, které mají větší topologickou dimenzi než jedna. Kupříkladu Hilbertova křivka je spojité zobrazení úsečky na čtverec, t.j. spojitá křivka, která vyplní celý (dvou-rozměrný) čtverec.

Hilbert curve.png

Na obrázku je prvních 6 iterací kontrukce Hilbertovy křivky. Hilbertova křivka je pak limitou těchto křivek. Je spojitá, ale není prostá. Její složky jsou spojité funkce, které nemají derivaci v žádném bodě. Jiný známý příklad křivky, která vyplní čtverec, je tzv. Sierpinského křivka. Klasifikace, který topologický prostor je spojitým obrazem intervalu [0,1], řeší tzv. Hahn–Mazurkiewiczova věta:

Speciálně tedy každá kompaktní souvislá varieta se dá "vyplnit" křivkou.

Příklady

Krivka explicitne.png Krivka parametricky.png Krivka aprox.png Krivka inter.png

Související články

Literatura

Externí odkazy

Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/K%C5%99ivka“