V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!

Kružnice připsaná

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(++)
 
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Kružnice připsaná|700}}
+
[[Soubor:Excircles and Nagel point.jpg|thumb|400px|Kružnice připsané a Nagelův bod]]
 +
'''[[Kružnice]] připsaná''' [[trojúhelník]]u se dotýká jedné jeho [[strana (geometrie)|strany]] a přímek, na nichž leží dvě zbývající strany trojúhelníku. Každý trojúhelník má tři kružnice připsané.
 +
== Vlastnosti ==
 +
* Střed kružnice připsané leží na [[osa|ose]] vnitřního úhlu, ležícího proti straně, které se kružnice připsaná dotýká.
 +
* Střed kružnice připsané leží na [[průsečík]]u os dvou vedlejších úhlů, ležících při straně, které se kružnice připsaná dotýká.
 +
* Poloměr kružnice připsané je kolmá vzdálenost středu od jedné strany trojúhelníka.
 +
* Všechny tři kružnice připsané mají vnější dotyk s [[kružnice devíti bodů|kružnicí devíti bodů]].
 +
* Spojnice dotykových bodů kružnic připsaných a protějších vrcholů trojúhelníka se protínají v jednom bodě, který se nazývá '''Nagelův bod'''. Nagelův bod vždy leží uvnitř trojúhelníka.
 +
 +
== Popis obrázku ==
 +
Kružnice připsané a Nagelův bod:
 +
* ΔABC
 +
* a, b, c – strany
 +
* o<sub>a</sub>, o<sub>b</sub>, o<sub>c</sub> – osy úhlů
 +
* v<sub>a</sub>, v<sub>b</sub>, v<sub>c</sub> – osy vedlejších úhlů
 +
* P<sub>a</sub>, P<sub>b</sub>, P<sub>c</sub> – průsečíky os úhlů a vedlejších úhlů, středy kružnic připsaných
 +
* p<sub>a</sub>, p<sub>b</sub>, p<sub>c</sub> – kružnice připsané
 +
* k<sub>a</sub>, k<sub>b</sub>, k<sub>c</sub> – kolmice ze středů kružnic připsaných na strany
 +
* K<sub>a</sub>, K<sub>b</sub>, K<sub>c</sub> – dotykové body
 +
* AK<sub>a</sub>, BK<sub>b</sub>, CK<sub>c</sub> – spojnice dotykových bodů s protějšími vrcholy
 +
* N – průsečík spojnic, Nagelův bod
 +
 +
== Související články ==
 +
* [[Kružnice opsaná]]
 +
* [[Kružnice vepsaná]]
 +
 +
== Literatura ==
 +
* {{Citace monografie
 +
| příjmení = Švrček
 +
| jméno = Jaroslav
 +
| příjmení2 = Vanžura
 +
| jméno2 = Jiří
 +
| titul = Geometrie trojúhelníka
 +
| vydavatel = Nakladatelství technické literatury
 +
| místo = Praha
 +
| rok = 1988
 +
| isbn =
 +
| kapitola =
 +
| strany =
 +
}}
 +
 +
 +
{{Článek z Wikipedie}}
[[Kategorie:Geometrie]]
[[Kategorie:Geometrie]]
[[Kategorie:Kružnice]]
[[Kategorie:Kružnice]]
[[Kategorie:Trojúhelník]]
[[Kategorie:Trojúhelník]]

Aktuální verze z 14. 6. 2021, 11:55

Kružnice připsané a Nagelův bod

Kružnice připsaná trojúhelníku se dotýká jedné jeho strany a přímek, na nichž leží dvě zbývající strany trojúhelníku. Každý trojúhelník má tři kružnice připsané.

Obsah

Vlastnosti

  • Střed kružnice připsané leží na ose vnitřního úhlu, ležícího proti straně, které se kružnice připsaná dotýká.
  • Střed kružnice připsané leží na průsečíku os dvou vedlejších úhlů, ležících při straně, které se kružnice připsaná dotýká.
  • Poloměr kružnice připsané je kolmá vzdálenost středu od jedné strany trojúhelníka.
  • Všechny tři kružnice připsané mají vnější dotyk s kružnicí devíti bodů.
  • Spojnice dotykových bodů kružnic připsaných a protějších vrcholů trojúhelníka se protínají v jednom bodě, který se nazývá Nagelův bod. Nagelův bod vždy leží uvnitř trojúhelníka.

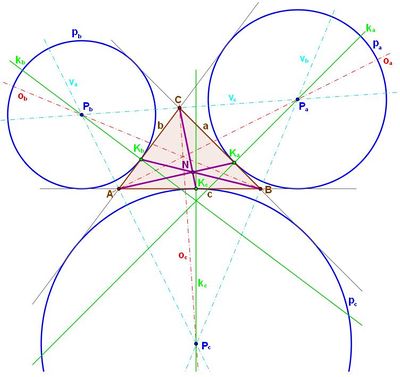
Popis obrázku

Kružnice připsané a Nagelův bod:

  • ΔABC
  • a, b, c – strany
  • oa, ob, oc – osy úhlů
  • va, vb, vc – osy vedlejších úhlů
  • Pa, Pb, Pc – průsečíky os úhlů a vedlejších úhlů, středy kružnic připsaných
  • pa, pb, pc – kružnice připsané
  • ka, kb, kc – kolmice ze středů kružnic připsaných na strany
  • Ka, Kb, Kc – dotykové body
  • AKa, BKb, CKc – spojnice dotykových bodů s protějšími vrcholy
  • N – průsečík spojnic, Nagelův bod

Související články

Literatura

  • ŠVRČEK, Jaroslav; VANŽURA, Jiří. Geometrie trojúhelníka. Praha : Nakladatelství technické literatury, 1988.  


Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/Kru%C5%BEnice_p%C5%99ipsan%C3%A1“