The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 24, 2026
(shortly after the 2026 Winter Olympics).

Montpellierský oblouk

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Výrazné vylepšení)
 
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Montpellierský oblouk|700}}
+
'''Montpellierský oblouk''' je jeden z [[konusoid]]ů, jako řídicí [[křivka|křivky]] jsou polokružnice, dále [[přímka]] rovnoběžná s [[rovina|rovinou]] této polokružnice (ale neležící v ní) a pak [[přímka]] procházející středem polokružnice a kolmá k její [[rovina|rovině]]. Plocha je tvořena přímkami, které protínají všechny tři [[řídicí křivka|řídicí křivky]]. Používá se jako [[přechodová plocha]] např. mezi čtvercem a kružnicí, což je častý případ ve [[vzduchotechnika|vzduchotechnice]].
-
 
+
 
 +
 
 +
<gallery widths="384" heights="267">
 +
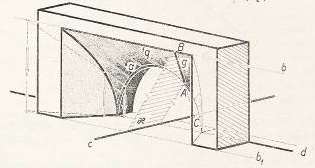
  Image:Montpelliersky_oblouk1.jpg|Montpellierský oblouk v ruční kresbě
 +
  Image:Montpelliersky_oblouk2.jpg|Montpellierský oblouk nakreslený počítačem
 +
</gallery>
 +
 
 +
== Externí odkazy ==
 +
* [http://www.geometrie.wz.cz/index%20II.html Stránky J. Ryšavého]
 +
 
 +
 
 +
{{Článek z Wikipedie}}
[[Kategorie:Geometrie]]
[[Kategorie:Geometrie]]
 +
[[Kategorie:Montpellier]]

Aktuální verze z 23. 2. 2014, 23:52

Montpellierský oblouk je jeden z konusoidů, jako řídicí křivky jsou polokružnice, dále přímka rovnoběžná s rovinou této polokružnice (ale neležící v ní) a pak přímka procházející středem polokružnice a kolmá k její rovině. Plocha je tvořena přímkami, které protínají všechny tři řídicí křivky. Používá se jako přechodová plocha např. mezi čtvercem a kružnicí, což je častý případ ve vzduchotechnice.


Montpellierský oblouk v ruční kresbě

Montpellierský oblouk nakreslený počítačem

Externí odkazy


Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/Montpelliersk%C3%BD_oblouk“