Multimediaexpo.cz je již 18 let na českém internetu !!
Lichoběžník
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 6: | Řádka 6: | ||
Úhlopříčky obecného lichoběžníku se navzájem nepůlí a nemusí se protínat na střední příčce lichoběžníku. | Úhlopříčky obecného lichoběžníku se navzájem nepůlí a nemusí se protínat na střední příčce lichoběžníku. | ||
Neexistuje pravoúhlý rovnoramenný lichoběžník. | Neexistuje pravoúhlý rovnoramenný lichoběžník. | ||
| - | Mají-li nerovnoběžné strany stejnou velikost, tzn. <big>\(|AD|=|BC|</ | + | Mají-li nerovnoběžné strany stejnou velikost, tzn. <big>\(|AD|=|BC|\)</big>, pak se jedná o ''rovnoramenný lichoběžník''. Rovnoramenný lichoběžník je [[tětivový čtyřúhelník|tětivovým čtyřúhelníkem]] – součet velikostí protilehlých úhlů je přímý úhel. |
| - | Velikost střední příčky lichoběžníku <big>\(s=\frac{a+c}{2}</ | + | Velikost střední příčky lichoběžníku <big>\(s=\frac{a+c}{2}\)</big> |
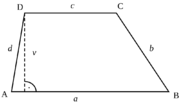
| - | Obsah dle obrázku vpravo <big>\(S = \frac{(a+c) \cdot v}{2}</ | + | Obsah dle obrázku vpravo <big>\(S = \frac{(a+c) \cdot v}{2}\)</big> |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:52
Lichoběžník je geometrický útvar, čtyřúhelník vymezený právě jednou dvojicí rovnoběžných stran.
Názvy stran
Názvy stran se podobají názvům rovnoramenného trojúhelníku, jen s tím rozdílem, že má dvě základny. Dvě protilehlé strany vzájemně rovnoběžné se nazývají základnami a zbývající dvojice různoběžných stran se nazývá rameny...
Vlastnosti
Úhlopříčky obecného lichoběžníku se navzájem nepůlí a nemusí se protínat na střední příčce lichoběžníku. Neexistuje pravoúhlý rovnoramenný lichoběžník. Mají-li nerovnoběžné strany stejnou velikost, tzn. \(|AD|=|BC|\), pak se jedná o rovnoramenný lichoběžník. Rovnoramenný lichoběžník je tětivovým čtyřúhelníkem – součet velikostí protilehlých úhlů je přímý úhel. Velikost střední příčky lichoběžníku \(s=\frac{a+c}{2}\) Obsah dle obrázku vpravo \(S = \frac{(a+c) \cdot v}{2}\)
Související články
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |