V pondělí 16. září 2024 začala naše další
nová soutěž o nejlepší webovou stránku !!
Proto neváhejte a začněte rychle soutěžit o lákavé ceny !!
nová soutěž o nejlepší webovou stránku !!
Proto neváhejte a začněte rychle soutěžit o lákavé ceny !!
Hyperboloid
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
m (1 revizi) |
(+ Masivní vylepšení) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 1: | Řádka 1: | ||
| - | + | [[Soubor:HyperboloidOfOneSheet.png|thumb|240px|Jednodílný hyperboloid]] | |
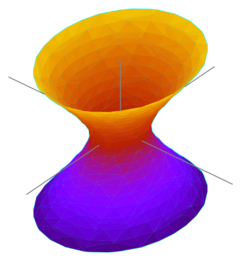
| + | '''Hyperboloid''' je [[plocha]] druhého stupně, neboli kvadratická plocha – [[kvadrika]]. Jsou dva druhy hyperboloidů, jednodílný a dvojdílný. | ||
| + | Má tři navzájem kolmé roviny souměrnosti, které se protínají ve třech přímkách, jež nazýváme osami hyperboloidu. Jejich průsečík je středem souměrnosti. Rotační hyperboloid má navíc osu souměrnosti. | ||
| + | |||
| + | [[Jednodílný hyperboloid]] je složen z [[přímka|přímek]], je to [[přímková plocha]] a proto nalézá uplatnění ve stavebnictví, např. u chladicích věží elektráren. | ||
| + | |||
| + | == Související články == | ||
| + | * [[Ještěd (hotel a vysílač)|Ještěd věž]] | ||
| + | * [[Televizní věž v Kantonu]] | ||
| + | * [[Šuchovova věž]] | ||
| + | * [[Borůvka (rozhledna)]] | ||
| + | * [[Slunečná (rozhledna)]] | ||
| + | |||
| + | == Externí odkazy == | ||
| + | |||
| + | |||
| + | {{commonscat|Hyperboloid}}{{Článek z Wikipedie}} | ||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
[[Kategorie:Prostorové geometrické útvary]] | [[Kategorie:Prostorové geometrické útvary]] | ||
Aktuální verze z 11. 12. 2016, 20:29
Hyperboloid je plocha druhého stupně, neboli kvadratická plocha – kvadrika. Jsou dva druhy hyperboloidů, jednodílný a dvojdílný.
Má tři navzájem kolmé roviny souměrnosti, které se protínají ve třech přímkách, jež nazýváme osami hyperboloidu. Jejich průsečík je středem souměrnosti. Rotační hyperboloid má navíc osu souměrnosti.
Jednodílný hyperboloid je složen z přímek, je to přímková plocha a proto nalézá uplatnění ve stavebnictví, např. u chladicích věží elektráren.
Související články
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |