V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.

Ortický trojúhelník

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Masivní vylepšení)
 
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Ortický trojúhelník|700}}
+
'''Ortický [[trojúhelník]]''' je trojúhelník, který je tvořen spojnicemi pat [[výška (geometrie)|výšek]] trojúhelníka.
 +
== Vlastnosti ortického trojúhelníka ==
 +
*U [[ostroúhlý trojúhelník|ostroúhlého trojúhelníka]] leží celý ortický trojúhelník uvnitř jeho plochy, u [[tupoúhlý trojúhelník|tupoúhlého]] leží část ortického trojúhelníka mimo jeho plochu. [[Pravoúhlý trojúhelník]] svůj ortický trojúhelník nemá, protože jeho dvě paty výšek splývají.
 +
*Ortocentrum (průsečík výšek) ostroúhlého trojúhelníka je středem [[kružnice vepsaná|kružnice vepsané]] jeho ortickému trojúhelníku; ortocentrum tupoúhlého trojúhelníka je středem jedné z [[kružnice připsaná|kružnic připsaných]] jeho ortickému trojúhelníku.
 +
*Spojnice středu kružnice opsané a jednotlivých vrcholů trojúhelníka jsou kolmé k jednotlivým stranám jeho ortického trojúhelníka (tzv. ''Nagelova věta'').
 +
 +
== Taylorova kružnice ==
 +
Pokud z vrcholů ortického trojúhelníka spustíme kolmice na zbývající strany, dostaneme celkem šest bodů. Všechny tyto body leží na kružnici, která se nazývá '''Taylorova kružnice'''.<ref>{{Citace monografie
 +
| příjmení = Švrček
 +
| jméno = Jaroslav
 +
| příjmení2 = Vanžura
 +
| jméno2 = Jiří
 +
| titul = Geometrie trojúhelníka
 +
| vydavatel = Nakladatelství technické literatury
 +
| místo = Praha
 +
| rok = 1988
 +
| isbn =
 +
| kapitola =
 +
| strany = 73-75
 +
}}
 +
</ref> Její střed je zároveň středem kružnice vepsané příčkovému trojúhelníku ortického trojúhelníka. Taylorova kružnice je speciálním případem [[Tuckerova kružnice|Tuckerovy kružnice]].
 +
 +
== Popis obrázku ==
 +
[[File:Taylor Circle.JPG|right|500px|Ortický trojúhelník a Taylorova kružnice]]
 +
Taylorova kružnice:
 +
*ΔABC,
 +
*a, b, c – strany,
 +
*v<sub>a</sub>, v<sub>b</sub>, v<sub>c</sub> – výšky,
 +
*V<sub>a</sub>, V<sub>b</sub>, V<sub>c</sub> – paty výšek,
 +
*V – ortocentrum (průsečík výšek),
 +
*{{barva|#2E8B57|'''ΔV<sub>a</sub>V<sub>b</sub>V<sub>c</sub> – ortický trojúhelník'''}},
 +
*ΔT<sub>1</sub>T<sub>2</sub>T<sub>3</sub> – příčkový trojúhelník ortického trojúhelníka
 +
*t – kružnice vepsaná ΔT<sub>1</sub>T<sub>2</sub>T<sub>3</sub>
 +
*v<sub>a1</sub>, v<sub>a2</sub>, v<sub>b1</sub>, v<sub>b2</sub>, v<sub>c1</sub>, v<sub>c2</sub> – kolmice na strany a, b, c spuštěné z vrcholů  ΔV<sub>a</sub>V<sub>b</sub>V<sub>c</sub>
 +
*{{barva|#000080|'''k – Taylorova kružnice'''}},
 +
*K – střed kružnic k, t
 +
*V<sub>a1</sub>, V<sub>a2</sub>, V<sub>b1</sub>, V<sub>b2</sub>, V<sub>c1</sub>, V<sub>c2</sub> – průsečíky kolmic v<sub>a1</sub>, v<sub>a2</sub>, v<sub>b1</sub>, v<sub>b2</sub>, v<sub>c1</sub>, v<sub>c2</sub> a stran a, b, c, všechny leží na Taylorově kružnice
 +
 +
== Související články ==
 +
*[[Trojúhelník]]
 +
*[[Výška (geometrie)]]
 +
 +
== Reference ==
 +
<references />
 +
== Literatura ==
 +
*{{Citace monografie
 +
| příjmení = Švrček
 +
| jméno = Jaroslav
 +
| příjmení2 = Vanžura
 +
| jméno2 = Jiří
 +
| titul = Geometrie trojúhelníka
 +
| vydavatel = Nakladatelství technické literatury
 +
| místo = Praha
 +
| rok = 1988
 +
| isbn =
 +
| kapitola =
 +
| strany =
 +
}}
 +
 +
 +
{{Článek z Wikipedie}}
[[Kategorie:Trojúhelník]]
[[Kategorie:Trojúhelník]]

Aktuální verze z 24. 10. 2014, 10:28

Ortický trojúhelník je trojúhelník, který je tvořen spojnicemi pat výšek trojúhelníka.

Obsah

Vlastnosti ortického trojúhelníka

  • U ostroúhlého trojúhelníka leží celý ortický trojúhelník uvnitř jeho plochy, u tupoúhlého leží část ortického trojúhelníka mimo jeho plochu. Pravoúhlý trojúhelník svůj ortický trojúhelník nemá, protože jeho dvě paty výšek splývají.
  • Ortocentrum (průsečík výšek) ostroúhlého trojúhelníka je středem kružnice vepsané jeho ortickému trojúhelníku; ortocentrum tupoúhlého trojúhelníka je středem jedné z kružnic připsaných jeho ortickému trojúhelníku.
  • Spojnice středu kružnice opsané a jednotlivých vrcholů trojúhelníka jsou kolmé k jednotlivým stranám jeho ortického trojúhelníka (tzv. Nagelova věta).

Taylorova kružnice

Pokud z vrcholů ortického trojúhelníka spustíme kolmice na zbývající strany, dostaneme celkem šest bodů. Všechny tyto body leží na kružnici, která se nazývá Taylorova kružnice.[1] Její střed je zároveň středem kružnice vepsané příčkovému trojúhelníku ortického trojúhelníka. Taylorova kružnice je speciálním případem Tuckerovy kružnice.

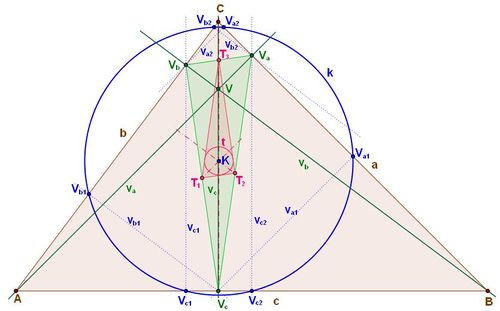
Popis obrázku

Ortický trojúhelník a Taylorova kružnice

Taylorova kružnice:

  • ΔABC,
  • a, b, c – strany,
  • va, vb, vc – výšky,
  • Va, Vb, Vc – paty výšek,
  • V – ortocentrum (průsečík výšek),
  • ΔVaVbVc – ortický trojúhelník,
  • ΔT1T2T3 – příčkový trojúhelník ortického trojúhelníka
  • t – kružnice vepsaná ΔT1T2T3
  • va1, va2, vb1, vb2, vc1, vc2 – kolmice na strany a, b, c spuštěné z vrcholů ΔVaVbVc
  • k – Taylorova kružnice,
  • K – střed kružnic k, t
  • Va1, Va2, Vb1, Vb2, Vc1, Vc2 – průsečíky kolmic va1, va2, vb1, vb2, vc1, vc2 a stran a, b, c, všechny leží na Taylorově kružnice

Související články

Reference

  1. ↑ ŠVRČEK, Jaroslav; VANŽURA, Jiří. Geometrie trojúhelníka. Praha : Nakladatelství technické literatury, 1988. S. 73-75.  

Literatura

  • ŠVRČEK, Jaroslav; VANŽURA, Jiří. Geometrie trojúhelníka. Praha : Nakladatelství technické literatury, 1988.  


Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/Ortick%C3%BD_troj%C3%BAheln%C3%ADk“