The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Kruhový oblouk
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Vylepšení) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 6: | Řádka 6: | ||
== Délka oblouku == | == Délka oblouku == | ||
Délka [[kružnice]] = 2πr | Délka [[kružnice]] = 2πr | ||
| - | * Délka oblouku příslušícího středovému úhlu 1°: < | + | * Délka oblouku příslušícího středovému úhlu 1°: <big>\(\frac{\pi r}{180}\)</big> |
| - | * Délka oblouku příslušícího středovému úhlu 1rad: < | + | * Délka oblouku příslušícího středovému úhlu 1rad: <big>\(r\)</big> |
| - | * Délka oblouku příslušícího úhlu θ (ve [[stupeň (úhel)|stupních]]): < | + | * Délka oblouku příslušícího úhlu θ (ve [[stupeň (úhel)|stupních]]): <big>\(\frac{2 \theta\pi r}{360^\circ}\)</big> |
| - | * Délka oblouku příslušícího úhlu θ (v [[radián]]ech): < | + | * Délka oblouku příslušícího úhlu θ (v [[radián]]ech): <big>\(\theta r\)</big> |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:52
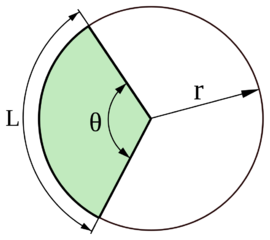
Kruhový oblouk je část obvodu kružnice, příslušná určitému středovému úhlu θ.
Je vymezen třemi body. Dva jsou okrajové a jeden upřesňující. Pokud vynecháme (neznáme) upřesňující bod a známe některou další charakteristiku kružnice (např. poloměr nebo obvod ap.), získáme dvě řešení (konvexní a nekonvexní).
Délka oblouku
Délka kružnice = 2πr
- Délka oblouku příslušícího středovému úhlu 1°: \(\frac{\pi r}{180}\)
- Délka oblouku příslušícího středovému úhlu 1rad: \(r\)
- Délka oblouku příslušícího úhlu θ (ve stupních): \(\frac{2 \theta\pi r}{360^\circ}\)
- Délka oblouku příslušícího úhlu θ (v radiánech): \(\theta r\)
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |