V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!

Montpellierský oblouk

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Výrazné vylepšení)
 
(Není zobrazena jedna mezilehlá verze.)
Řádka 1: Řádka 1:
-
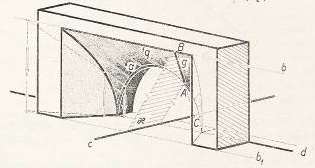
{{Wikipedia-cs|Montpellierský oblouk|700}}
+
'''Montpellierský oblouk''' je jeden z [[konusoid]]ů, jako řídicí [[křivka|křivky]] jsou polokružnice, dále [[přímka]] rovnoběžná s [[rovina|rovinou]] této polokružnice (ale neležící v ní) a pak [[přímka]] procházející středem polokružnice a kolmá k její [[rovina|rovině]]. Plocha je tvořena přímkami, které protínají všechny tři [[řídicí křivka|řídicí křivky]]. Používá se jako [[přechodová plocha]] např. mezi čtvercem a kružnicí, což je častý případ ve [[vzduchotechnika|vzduchotechnice]].
-
 
+
 
 +
 
 +
<gallery widths="384" heights="267">
 +
  Image:Montpelliersky_oblouk1.jpg|Montpellierský oblouk v ruční kresbě
 +
  Image:Montpelliersky_oblouk2.jpg|Montpellierský oblouk nakreslený počítačem
 +
</gallery>
 +
 
 +
== Externí odkazy ==
 +
* [http://www.geometrie.wz.cz/index%20II.html Stránky J. Ryšavého]
 +
 
 +
 
 +
{{Článek z Wikipedie}}
[[Kategorie:Geometrie]]
[[Kategorie:Geometrie]]
 +
[[Kategorie:Montpellier]]

Aktuální verze z 23. 2. 2014, 23:52

Montpellierský oblouk je jeden z konusoidů, jako řídicí křivky jsou polokružnice, dále přímka rovnoběžná s rovinou této polokružnice (ale neležící v ní) a pak přímka procházející středem polokružnice a kolmá k její rovině. Plocha je tvořena přímkami, které protínají všechny tři řídicí křivky. Používá se jako přechodová plocha např. mezi čtvercem a kružnicí, což je častý případ ve vzduchotechnice.


Montpellierský oblouk v ruční kresbě

Montpellierský oblouk nakreslený počítačem

Externí odkazy


Citováno z „http://www1fdc.multimediaexpo.cz/mmecz/index.php/Montpelliersk%C3%BD_oblouk“