Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Šroubovice
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 1: | Řádka 1: | ||
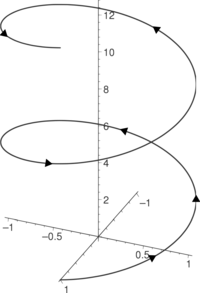
| - | [[Soubor:Helix.png|thumb|200px|Příklad šroubovice se souřadnicemi (<big>\((\cos t, \sin t, t)</ | + | [[Soubor:Helix.png|thumb|200px|Příklad šroubovice se souřadnicemi (<big>\((\cos t, \sin t, t)\)</big> pro <big>\(t\)</big> od 0 do <big>\(4\pi\)</big>]] |
'''Šroubovice''' je trojrozměrná [[křivka]], která má tu vlastnost, že [[tečna|tečny]] ve všech jejích bodech mají stejný [[úhel]] vzhledem k pevně dané [[přímka|přímce]] nazývané ''osa'' šroubovice. Odpovídá pohybu bodu, který se zároveň pohybuje rovnoměrně podél oné osy a zároveň ji rovnoměrně obíhá po [[kružnice|kružnici]]. Úsek odpovídající jednomu oběhu kolem kružnice se přitom nazývá ''závit'' a vzdálenost jeho koncových bodů se nazývá ''výška závitu''. Šroubovici lze popsat třemi parametry: [[poloměr]]em zmíněné kružnice, výškou závitu a tím, zda se jedná o šroubovici pravotočivou, nebo levotočivou. Zmíněný poloměr je zároveň poloměrem [[válcová plocha|rotační válcové plochy]], v které celá šroubovice leží. | '''Šroubovice''' je trojrozměrná [[křivka]], která má tu vlastnost, že [[tečna|tečny]] ve všech jejích bodech mají stejný [[úhel]] vzhledem k pevně dané [[přímka|přímce]] nazývané ''osa'' šroubovice. Odpovídá pohybu bodu, který se zároveň pohybuje rovnoměrně podél oné osy a zároveň ji rovnoměrně obíhá po [[kružnice|kružnici]]. Úsek odpovídající jednomu oběhu kolem kružnice se přitom nazývá ''závit'' a vzdálenost jeho koncových bodů se nazývá ''výška závitu''. Šroubovici lze popsat třemi parametry: [[poloměr]]em zmíněné kružnice, výškou závitu a tím, zda se jedná o šroubovici pravotočivou, nebo levotočivou. Zmíněný poloměr je zároveň poloměrem [[válcová plocha|rotační válcové plochy]], v které celá šroubovice leží. | ||
| Řádka 16: | Řádka 16: | ||
== Parametrické rovnice == | == Parametrické rovnice == | ||
V [[kartézská soustava souřadnic|kartézské soustavě souřadnic]] má obecná pravotočivá šroubovice, jejíž osou je souřadná osa ''z'', základní [[parametrizace|parametrické]] rovnice: | V [[kartézská soustava souřadnic|kartézské soustavě souřadnic]] má obecná pravotočivá šroubovice, jejíž osou je souřadná osa ''z'', základní [[parametrizace|parametrické]] rovnice: | ||
| - | :<big>\(x=a\cos t</ | + | :<big>\(x=a\cos t\)</big> |
| - | :<big>\(y=a\sin t</ | + | :<big>\(y=a\sin t\)</big> |
| - | :<big>\(z=bt</ | + | :<big>\(z=bt\)</big> |
kde hodnota ''a'' představuje poloměr rotační válcové plochy, hodnotou ''b'' je ovlivněna výška závitu, která je 2''[[číslo pí|πb]]'', a ''t'' je parametr z oboru reálných čísel. Vzhledem k rotačnímu charakteru je jednodušší vyjádření této šroubovice ve [[válcová soustava souřadnic|válcové soustavě souřadnic]], kde odpovídá parametrizaci: | kde hodnota ''a'' představuje poloměr rotační válcové plochy, hodnotou ''b'' je ovlivněna výška závitu, která je 2''[[číslo pí|πb]]'', a ''t'' je parametr z oboru reálných čísel. Vzhledem k rotačnímu charakteru je jednodušší vyjádření této šroubovice ve [[válcová soustava souřadnic|válcové soustavě souřadnic]], kde odpovídá parametrizaci: | ||
| - | :<big>\(r=a</ | + | :<big>\(r=a\)</big> |
| - | :<big>\(\varphi=t</ | + | :<big>\(\varphi=t\)</big> |
| - | :<big>\(z=bt</ | + | :<big>\(z=bt\)</big> |
== Šroubovice v praxi == | == Šroubovice v praxi == | ||
Aktuální verze z 14. 8. 2022, 14:54
Šroubovice je trojrozměrná křivka, která má tu vlastnost, že tečny ve všech jejích bodech mají stejný úhel vzhledem k pevně dané přímce nazývané osa šroubovice. Odpovídá pohybu bodu, který se zároveň pohybuje rovnoměrně podél oné osy a zároveň ji rovnoměrně obíhá po kružnici. Úsek odpovídající jednomu oběhu kolem kružnice se přitom nazývá závit a vzdálenost jeho koncových bodů se nazývá výška závitu. Šroubovici lze popsat třemi parametry: poloměrem zmíněné kružnice, výškou závitu a tím, zda se jedná o šroubovici pravotočivou, nebo levotočivou. Zmíněný poloměr je zároveň poloměrem rotační válcové plochy, v které celá šroubovice leží.
Šikmým průmětem šroubovice do roviny kolmé na její osu vzniká cykloida[1], kolmým průmětem do stejné roviny vzniká kružnice.
Obsah |
Parametrické rovnice
V kartézské soustavě souřadnic má obecná pravotočivá šroubovice, jejíž osou je souřadná osa z, základní parametrické rovnice:
- \(x=a\cos t\)
- \(y=a\sin t\)
- \(z=bt\)
kde hodnota a představuje poloměr rotační válcové plochy, hodnotou b je ovlivněna výška závitu, která je 2πb, a t je parametr z oboru reálných čísel. Vzhledem k rotačnímu charakteru je jednodušší vyjádření této šroubovice ve válcové soustavě souřadnic, kde odpovídá parametrizaci:
- \(r=a\)
- \(\varphi=t\)
- \(z=bt\)
Šroubovice v praxi
Tvar šroubovice je užívaný v praxi například pro závity nebo šroubovité pružiny, odpovídá tvaru zábradlí na točitém schodišti. Významná je také dvoušroubovice, dvojice šroubovic se stejnými parametry a stejnou osou po této ose vůči sobě posunutá – tuto podobu mají molekuly DNA.
Reference
- ↑ SÝKORA, Antonín. Šikmý průmět šroubovice. Časopis pro pěstování mathematiky a fysiky, 1905, čís. 1, s. 91-92. Dostupné online.
Externí odkazy
|
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |