Weierstrassova funkce
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Masivní vylepšení) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 1: | Řádka 1: | ||
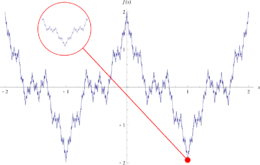
| - | [[Soubor:Weierf.png|thumb|260px|Weierstrassova funkce s konstantami < | + | [[Soubor:Weierf.png|thumb|260px|Weierstrassova funkce s konstantami <big>\(a=0,5\)</big>; <big>\(b=3\)</big>.]] |
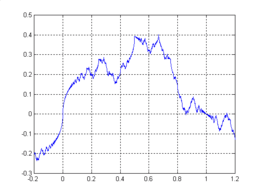
[[Soubor:WeierstrassFunction.png|260px|thumb|Ukázka soběpodobnosti.]] | [[Soubor:WeierstrassFunction.png|260px|thumb|Ukázka soběpodobnosti.]] | ||
'''Weierstrassova funkce''', pojmenovaná po [[Německo|německém]] matematikovi Karlu Weierstrassovi (1815–1897), je [[matematika|matematická]] [[Funkce (matematika)|funkce]], která je ve všech [[bod]]ech [[Spojitá funkce|spojitá]], ale v žádném bodě nemá [[derivace|derivaci]]. | '''Weierstrassova funkce''', pojmenovaná po [[Německo|německém]] matematikovi Karlu Weierstrassovi (1815–1897), je [[matematika|matematická]] [[Funkce (matematika)|funkce]], která je ve všech [[bod]]ech [[Spojitá funkce|spojitá]], ale v žádném bodě nemá [[derivace|derivaci]]. | ||
| Řádka 10: | Řádka 10: | ||
* Podle původní publikace ([http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=00770001&seq=&view=50&frames=0&pagenum=97 http://historical.library.cornell.edu/…]) a [http://planetmath.org/encyclopedia/WeierstrassFunction.html http://planetmath.org/…]: | * Podle původní publikace ([http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=00770001&seq=&view=50&frames=0&pagenum=97 http://historical.library.cornell.edu/…]) a [http://planetmath.org/encyclopedia/WeierstrassFunction.html http://planetmath.org/…]: | ||
| - | :< | + | :<big>\(f(x) = \sum_{n=0}^\infty a^n\cos(b^n\pi x)\)</big> |
| - | :kde < | + | :kde <big>\(0<a<1\)</big>, <big>\(b\)</big> je kladné liché číslo a konstanty splňují následující podmínku. |
| - | :< | + | :<big>\( ab > 1+\frac{3}{2} \pi\)</big> |
| - | :Později bylo dokázáno, že poslední uvedenou podmínku lze nahradit podmínkou < | + | :Později bylo dokázáno, že poslední uvedenou podmínku lze nahradit podmínkou <big>\(ab \ge 1\)</big>. |
* Podle [http://mathworld.wolfram.com/WeierstrassFunction.html http://mathworld.wolfram.com/…]: | * Podle [http://mathworld.wolfram.com/WeierstrassFunction.html http://mathworld.wolfram.com/…]: | ||
| - | [[Soubor:Riemannf.png|thumb|260px|Riemannova funkce, < | + | [[Soubor:Riemannf.png|thumb|260px|Riemannova funkce, <big>\(a=2\)</big>.]] |
| - | :< | + | :<big>\(f_a(x) = \sum_{k=1}^\infty \frac{ \sin(\pi k^a x) } {\pi k^a} \,\)</big> |
| - | :přičemž údajně podle původní publikace < | + | :přičemž údajně podle původní publikace <big>\(a = 2\)</big>. Tato funkce má však v určitých izolovaných bodech konečné derivace. Podle jiných zdrojů<ref>http://epubl.ltu.se/1402-1617/2003/320/index-en.html</ref> je tato funkce nazývána ''Riemannova'', neboť podle Weierstrasse ji Bernhard Riemann uváděl na svých přednáškách okolo roku 1861. |
* Lze nalézt i jiné tvary nebo konkrétní konstanty.<ref name="conroy" /><ref>http://pirate.shu.edu/~wachsmut/ira/cont/fp_weier.html</ref> | * Lze nalézt i jiné tvary nebo konkrétní konstanty.<ref name="conroy" /><ref>http://pirate.shu.edu/~wachsmut/ira/cont/fp_weier.html</ref> | ||
Aktuální verze z 14. 8. 2022, 14:54
Weierstrassova funkce, pojmenovaná po německém matematikovi Karlu Weierstrassovi (1815–1897), je matematická funkce, která je ve všech bodech spojitá, ale v žádném bodě nemá derivaci.
Funkce se chová jako fraktál, neboť zvětšené části grafu a původní graf jsou podobné.[1]
Definice
Weierstrassova funkce bývá uváděna v různých tvarech s různými konstantami.
- Podle původní publikace (http://historical.library.cornell.edu/…) a http://planetmath.org/…:
- \(f(x) = \sum_{n=0}^\infty a^n\cos(b^n\pi x)\)
- kde \(0<a<1\), \(b\) je kladné liché číslo a konstanty splňují následující podmínku.
- \( ab > 1+\frac{3}{2} \pi\)
- Později bylo dokázáno, že poslední uvedenou podmínku lze nahradit podmínkou \(ab \ge 1\).
- \(f_a(x) = \sum_{k=1}^\infty \frac{ \sin(\pi k^a x) } {\pi k^a} \,\)
- přičemž údajně podle původní publikace \(a = 2\). Tato funkce má však v určitých izolovaných bodech konečné derivace. Podle jiných zdrojů[2] je tato funkce nazývána Riemannova, neboť podle Weierstrasse ji Bernhard Riemann uváděl na svých přednáškách okolo roku 1861.
Související články
Reference
- ↑ 1,0 1,1 Příklad Weierstrassovy funkce, ukázka soběpodobnosti: http://www.math.washington.edu/…
- ↑ http://epubl.ltu.se/1402-1617/2003/320/index-en.html
- ↑ http://pirate.shu.edu/~wachsmut/ira/cont/fp_weier.html
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |