Kvadratická funkce
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Nový článek) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 1: | Řádka 1: | ||
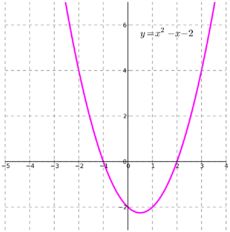
| - | [[File:Polynomialdeg2.png|thumb|230px|<center>< | + | [[File:Polynomialdeg2.png|thumb|230px|<center><big>\(x^2 - x - 2\!\)</big></center>]] |
'''Kvadratická funkce''' je taková [[Funkce (matematika)|funkce]], jejíž hodnota se mění úměrně druhé [[Umocňování|mocnině]] nezávislé [[proměnná|proměnné]]. | '''Kvadratická funkce''' je taková [[Funkce (matematika)|funkce]], jejíž hodnota se mění úměrně druhé [[Umocňování|mocnině]] nezávislé [[proměnná|proměnné]]. | ||
| - | Například funkce < | + | Například funkce <big>\(y = -2x^2 + 5x + {1 \over 2}\)</big> je kvadratická. |
| - | Ryze kvadratická funkce je pak funkce bez lineárního členu x, například < | + | Ryze kvadratická funkce je pak funkce bez lineárního členu x, například <big>\(y = 3x^2 - 10\)</big>. |
== Definice == | == Definice == | ||
| - | Funkce ''f'' je kvadratická, pokud ji lze vyjádřit ve tvaru < | + | Funkce ''f'' je kvadratická, pokud ji lze vyjádřit ve tvaru <big>\(f(x) = a \cdot x^2 + b \cdot x + c\)</big>,<br />kde ''a'', ''b'' i ''c'' jsou [[konstanta|konstanty]] a <big>\(a \ne 0\)</big>. |
| - | [[Definiční obor]] kvadratické funkce je < | + | [[Definiční obor]] kvadratické funkce je <big>\(( - \infty, \infty )\)</big>. |
== Vlastnosti == | == Vlastnosti == | ||
* [[graf (funkce)|grafem]] kvadratické funkce je [[Parabola (matematika)|parabola]] | * [[graf (funkce)|grafem]] kvadratické funkce je [[Parabola (matematika)|parabola]] | ||
* kvadratická funkce má v každém bodě [[derivace|derivaci]] | * kvadratická funkce má v každém bodě [[derivace|derivaci]] | ||
| - | ** příklad: funkce < | + | ** příklad: funkce <big>\(f(x) = 5x^2 + 3x - 6\)</big> má derivaci <big>\(f'(x) = 10x + 3\)</big> |
* [[primitivní funkce]] ke kvadratické funkci je funkce [[kubická funkce|kubická]] | * [[primitivní funkce]] ke kvadratické funkci je funkce [[kubická funkce|kubická]] | ||
| - | ** příklad: < | + | ** příklad: <big>\(\int 5x^2 + 3x - 6 \, dx = {5 \over 3} x^3 + {3 \over 2}x^2 - 6x + C\)</big> |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:52
Kvadratická funkce je taková funkce, jejíž hodnota se mění úměrně druhé mocnině nezávislé proměnné.
Například funkce \(y = -2x^2 + 5x + {1 \over 2}\) je kvadratická.
Ryze kvadratická funkce je pak funkce bez lineárního členu x, například \(y = 3x^2 - 10\).
Definice
Funkce f je kvadratická, pokud ji lze vyjádřit ve tvaru \(f(x) = a \cdot x^2 + b \cdot x + c\),
kde a, b i c jsou konstanty a \(a \ne 0\).
Definiční obor kvadratické funkce je \(( - \infty, \infty )\).
Vlastnosti
- grafem kvadratické funkce je parabola
- kvadratická funkce má v každém bodě derivaci
- příklad: funkce \(f(x) = 5x^2 + 3x - 6\) má derivaci \(f'(x) = 10x + 3\)
- primitivní funkce ke kvadratické funkci je funkce kubická
- příklad: \(\int 5x^2 + 3x - 6 \, dx = {5 \over 3} x^3 + {3 \over 2}x^2 - 6x + C\)
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |