Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Eisensteinovo číslo
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 2: | Řádka 2: | ||
V [[matematika|matematice]] se jako '''Eisensteinova čísla''', pojmenovaná po Ferdinandu Eisensteinovi (1823 – 1852), označují [[komplexní číslo|komplexní čísla]] tvaru | V [[matematika|matematice]] se jako '''Eisensteinova čísla''', pojmenovaná po Ferdinandu Eisensteinovi (1823 – 1852), označují [[komplexní číslo|komplexní čísla]] tvaru | ||
| - | :<big>\(z = a + b\omega \,\!</ | + | :<big>\(z = a + b\omega \,\!\)</big> |
kde ''a'' a ''b'' jsou [[celé číslo|celá čísla]] a | kde ''a'' a ''b'' jsou [[celé číslo|celá čísla]] a | ||
| - | :<big>\(\omega = \frac{1}{2}(-1 + i\sqrt 3) = e^{2\pi i/3}</ | + | :<big>\(\omega = \frac{1}{2}(-1 + i\sqrt 3) = e^{2\pi i/3}\)</big> |
| - | je (komplexní) [[třetí odmocnina z jedné]]. Podobně jako [[Gaussovo číslo|Gaussova čísla]] tvoří čtvercovou mříž, tvoří Eisensteinova čísla trojúhelníkovou mříž. Jedná se o [[okruh celistvých čísel]] [[číselné těleso|číselného tělesa]] <big>\(\mathbb{Q}\left(\mathrm i\sqrt{3}\right)</ | + | je (komplexní) [[třetí odmocnina z jedné]]. Podobně jako [[Gaussovo číslo|Gaussova čísla]] tvoří čtvercovou mříž, tvoří Eisensteinova čísla trojúhelníkovou mříž. Jedná se o [[okruh celistvých čísel]] [[číselné těleso|číselného tělesa]] <big>\(\mathbb{Q}\left(\mathrm i\sqrt{3}\right)\)</big>. |
== Dělitelnost == | == Dělitelnost == | ||
| - | Na Eisensteinových číslech lze zavést [[dělitelnost]] stejně jako na celých číslech: <big>\(x</ | + | Na Eisensteinových číslech lze zavést [[dělitelnost]] stejně jako na celých číslech: <big>\(x\)</big> dělí <big>\(y\)</big> právě tehdy, existuje-li Eisensteinovo číslo <big>\(z\)</big> splňující <big>\(y=zx\)</big>. To umožňuje převést z celých čísel i koncept [[prvočíselnost]]i, a mluvit o [[Eisensteinův prvočinitel|Eisensteinových prvočíslech]]. |
| - | Mezi Eisensteinovými čísly je celkem šest [[jednotkový prvek|jednotek]] {±1, ±ω, ±ω<sup>2</sup>}, za Eisensteinova prvočíslo je tedy považováno každé takové Eisensteinovo číslo <big>\(z</ | + | Mezi Eisensteinovými čísly je celkem šest [[jednotkový prvek|jednotek]] {±1, ±ω, ±ω<sup>2</sup>}, za Eisensteinova prvočíslo je tedy považováno každé takové Eisensteinovo číslo <big>\(z\)</big>, které lze dělit pouze pouze jednotkami a prvky <big>\(uz\)</big>, kde <big>\(u\)</big> je nějaká z jednotek. |
Eisensteinova čísla tvoří [[komutativní okruh]]. Ten je dokonce [[eukleidovský obor|eukleidovský]], za eukleidovskou funkci je možno zvolit | Eisensteinova čísla tvoří [[komutativní okruh]]. Ten je dokonce [[eukleidovský obor|eukleidovský]], za eukleidovskou funkci je možno zvolit | ||
| - | :<big>\(N(a + b\,\omega) = a^2 - a b + b^2. \,\!</ | + | :<big>\(N(a + b\,\omega) = a^2 - a b + b^2. \,\!\)</big> |
Aktuální verze z 14. 8. 2022, 14:51
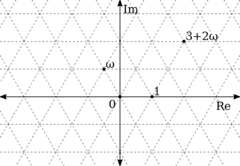
V matematice se jako Eisensteinova čísla, pojmenovaná po Ferdinandu Eisensteinovi (1823 – 1852), označují komplexní čísla tvaru
- \(z = a + b\omega \,\!\)
kde a a b jsou celá čísla a
- \(\omega = \frac{1}{2}(-1 + i\sqrt 3) = e^{2\pi i/3}\)
je (komplexní) třetí odmocnina z jedné. Podobně jako Gaussova čísla tvoří čtvercovou mříž, tvoří Eisensteinova čísla trojúhelníkovou mříž. Jedná se o okruh celistvých čísel číselného tělesa \(\mathbb{Q}\left(\mathrm i\sqrt{3}\right)\).
Dělitelnost
Na Eisensteinových číslech lze zavést dělitelnost stejně jako na celých číslech: \(x\) dělí \(y\) právě tehdy, existuje-li Eisensteinovo číslo \(z\) splňující \(y=zx\). To umožňuje převést z celých čísel i koncept prvočíselnosti, a mluvit o Eisensteinových prvočíslech.
Mezi Eisensteinovými čísly je celkem šest jednotek {±1, ±ω, ±ω2}, za Eisensteinova prvočíslo je tedy považováno každé takové Eisensteinovo číslo \(z\), které lze dělit pouze pouze jednotkami a prvky \(uz\), kde \(u\) je nějaká z jednotek.
Eisensteinova čísla tvoří komutativní okruh. Ten je dokonce eukleidovský, za eukleidovskou funkci je možno zvolit
- \(N(a + b\,\omega) = a^2 - a b + b^2. \,\!\)
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |
