The final launch of the Allmultimedia.org will take place on February 24, 2026
(shortly after the 2026 Winter Olympics).
Diskrétní graf
Z Multimediaexpo.cz
(+ Nový článek) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 3: | Řádka 3: | ||
== Definice == | == Definice == | ||
| - | Graf < | + | Graf <big>\( G = (V, E) \,\! \)</big> je '''diskrétní''', pokud <big>\(E = \emptyset \,\!\)</big>.<br /> |
| - | Diskrétní graf o < | + | Diskrétní graf o <big>\(n\)</big> vrcholech je obvykle označován symbolem <big>\( D_n \,\! \)</big>. |
== Význam == | == Význam == | ||
Aktuální verze z 14. 8. 2022, 14:51
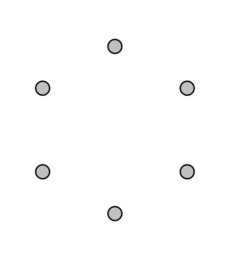
Diskrétní graf je matematický pojem z oboru teorie grafů označující takový graf, v němž žádné dva vrcholy nejsou spojené hranou.
Definice
Graf \( G = (V, E) \,\! \) je diskrétní, pokud \(E = \emptyset \,\!\).
Diskrétní graf o \(n\) vrcholech je obvykle označován symbolem \( D_n \,\! \).
Význam
Diskrétní graf je sám o sobě z pohledu teorie grafů poměrně nezajímavá struktura. Jeho význam (a důvod, proč jej vůbec definovat jako samostatný pojem) se projevuje ve chvíli, kdy uvažujeme o množině všech možných grafů na určité pevně dané množině vrcholů. V takovéto množině je diskrétní graf jejím nejmenším prvkem vzhledem k uspořádání relací "být podgrafem", tj. množina hran každého grafu je nadmnožinou množiny hran diskrétního grafu.
Od diskrétního grafu začínají mnohé grafové algoritmy - například Borůvkův hladový algoritmus pro hledání minimální kostry grafu.
Doplňkem diskrétního grafu je graf, který obsahuje všechny myslitelné hrany na dané množině vrcholů, tj. úplný graf.
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |