The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 24, 2026
(shortly after the 2026 Winter Olympics).
The final launch of the Allmultimedia.org will take place on February 24, 2026
(shortly after the 2026 Winter Olympics).
Tangentová věta
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Masivní vylepšení) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 3: | Řádka 3: | ||
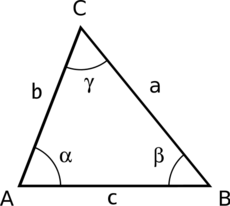
Pro každý trojúhelník ABC s vnitřními [[úhel|úhly]] α, β, γ a stranami ''a'', ''b'', ''c'' platí: | Pro každý trojúhelník ABC s vnitřními [[úhel|úhly]] α, β, γ a stranami ''a'', ''b'', ''c'' platí: | ||
| - | :< | + | :<big>\(\frac{a-b}{a+b}=\frac{\mathrm{tg}\, \frac{\alpha -\beta }{2}}{\mathrm{tg}\, \frac{\alpha +\beta }{2}}=\frac{\mathrm{tg}\, \frac{\alpha -\beta }{2}}{\mathrm{cotg}\, \frac{\gamma }{2}}</math> |
| - | :< | + | :<big>\(\frac{b-c}{b+c}=\frac{\mathrm{tg}\, \frac{\beta -\gamma }{2}}{\mathrm{tg}\, \frac{\beta +\gamma }{2}}=\frac{\mathrm{tg}\, \frac{\beta -\gamma }{2}}{\mathrm{cotg}\, \frac{\alpha }{2}}</math> |
| - | :< | + | :<big>\(\frac{c-a}{c+a}=\frac{\mathrm{tg}\, \frac{\gamma -\alpha }{2}}{\mathrm{tg}\, \frac{\gamma +\alpha }{2}}=\frac{\mathrm{tg}\, \frac{\gamma -\alpha }{2}}{\mathrm{cotg}\, \frac{\beta }{2}}</math> |
== Související články == | == Související články == | ||
Verze z 14. 8. 2022, 14:50
V trigonometrii je tangentová věta tvrzení o rovinných trojúhelnících.
Pro každý trojúhelník ABC s vnitřními úhly α, β, γ a stranami a, b, c platí:
- \(\frac{a-b}{a+b}=\frac{\mathrm{tg}\, \frac{\alpha -\beta }{2}}{\mathrm{tg}\, \frac{\alpha +\beta }{2}}=\frac{\mathrm{tg}\, \frac{\alpha -\beta }{2}}{\mathrm{cotg}\, \frac{\gamma }{2}}</math>
- \(\frac{b-c}{b+c}=\frac{\mathrm{tg}\, \frac{\beta -\gamma }{2}}{\mathrm{tg}\, \frac{\beta +\gamma }{2}}=\frac{\mathrm{tg}\, \frac{\beta -\gamma }{2}}{\mathrm{cotg}\, \frac{\alpha }{2}}</math>
- \(\frac{c-a}{c+a}=\frac{\mathrm{tg}\, \frac{\gamma -\alpha }{2}}{\mathrm{tg}\, \frac{\gamma +\alpha }{2}}=\frac{\mathrm{tg}\, \frac{\gamma -\alpha }{2}}{\mathrm{cotg}\, \frac{\beta }{2}}</math>
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |