Multimediaexpo.cz je již 18 let na českém internetu !!
Stupeň vrcholu
Z Multimediaexpo.cz
(+ Nový článek) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 4: | Řádka 4: | ||
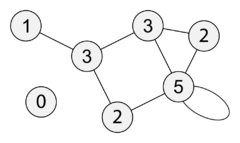
[[Soubor:UndirectedDegrees (Loop).png|240px|thumb|Neorientovaný graf s 6 vrcholy označenými jejich stupněm]] | [[Soubor:UndirectedDegrees (Loop).png|240px|thumb|Neorientovaný graf s 6 vrcholy označenými jejich stupněm]] | ||
| - | :< | + | :<big>\(deg(u) = \left | \{e\in\mathit{E} \mid u\in e\;\}\right |</math> |
U neorientovaného grafu je stupeň vrcholu počet hran, které do daného vrcholu zasahují. Koncové body [[Hrana (graf)|smyčky]] tvoří tentýž vrchol, proto se tato hrana počítá dvakrát. | U neorientovaného grafu je stupeň vrcholu počet hran, které do daného vrcholu zasahují. Koncové body [[Hrana (graf)|smyčky]] tvoří tentýž vrchol, proto se tato hrana počítá dvakrát. | ||
| Řádka 13: | Řádka 13: | ||
U orientovaného grafu se rozlišuje tzv. ''vstupní'' a ''výstupní'' stupeň vrcholu: | U orientovaného grafu se rozlišuje tzv. ''vstupní'' a ''výstupní'' stupeň vrcholu: | ||
* vstupní stupeň | * vstupní stupeň | ||
| - | :< | + | :<big>\(deg^+(u) = \left | \{e\in\mathit{E} \mid \exists v\in\mathit{V}\;:e = (v, u)\;\}\right |</math> |
* výstupní stupeň | * výstupní stupeň | ||
| - | :< | + | :<big>\(deg^-(u) = \left | \{e\in\mathit{E} \mid \exists v\in\mathit{V}\;:e = (u, v)\;\}\right |</math> |
U orientovaného grafu jsou hrany orientované, proto se vstupující hrana a vystupující hrany počítají zvlášť. Celkový stupeň uzlu je pak roven součtu vstupujících a vystupujících hran. | U orientovaného grafu jsou hrany orientované, proto se vstupující hrana a vystupující hrany počítají zvlášť. Celkový stupeň uzlu je pak roven součtu vstupujících a vystupujících hran. | ||
| Řádka 34: | Řádka 34: | ||
== Princip sudosti == | == Princip sudosti == | ||
| - | ''Tvrzení'': V neorientovaném grafu ''G = (V, E)'' platí < | + | ''Tvrzení'': V neorientovaném grafu ''G = (V, E)'' platí <big>\(\sum_{v\in\mathit{V}}deg(v) = 2\left |E\right |</math> |
''Důkaz'': Je to pouze vyjádření faktu, že každou hranu započítáváme dvakrát - jednou ve vrcholu, kde začíná, podruhé ve vrcholu, kde končí. | ''Důkaz'': Je to pouze vyjádření faktu, že každou hranu započítáváme dvakrát - jednou ve vrcholu, kde začíná, podruhé ve vrcholu, kde končí. | ||
| - | ''Poznámka'': Pro orientované grafy změníme levou stranu rovnosti v tvrzení na < | + | ''Poznámka'': Pro orientované grafy změníme levou stranu rovnosti v tvrzení na <big>\(\sum_{v\in\mathit{V}}\left (deg^+(v) + deg^-(v)\right )</math> |
''Důsledek'': Počet vrcholů s lichým stupněm je sudé číslo. Neboli „počet lidí, kteří si na večírku potřásli ruce s lichým počtem účastníků, je sudé číslo“. | ''Důsledek'': Počet vrcholů s lichým stupněm je sudé číslo. Neboli „počet lidí, kteří si na večírku potřásli ruce s lichým počtem účastníků, je sudé číslo“. | ||
Verze z 14. 8. 2022, 14:50
V teorii grafů se pojmem stupeň vrcholu (někdy též valence vrcholu) označuje počet hran, které do daného vrcholu zasahují. Stupeň vrcholu u se značí deg(u). Přesnější definice závisí na tom, zda je graf orientovaný nebo neorientovaný.
Obsah |
Neorientovaný graf
- \(deg(u) = \left | \{e\in\mathit{E} \mid u\in e\;\}\right |</math>
U neorientovaného grafu je stupeň vrcholu počet hran, které do daného vrcholu zasahují. Koncové body smyčky tvoří tentýž vrchol, proto se tato hrana počítá dvakrát.
Orientovaný graf
U orientovaného grafu se rozlišuje tzv. vstupní a výstupní stupeň vrcholu:
- vstupní stupeň
- \(deg^+(u) = \left | \{e\in\mathit{E} \mid \exists v\in\mathit{V}\;:e = (v, u)\;\}\right |</math>
- výstupní stupeň
- \(deg^-(u) = \left | \{e\in\mathit{E} \mid \exists v\in\mathit{V}\;:e = (u, v)\;\}\right |</math>
U orientovaného grafu jsou hrany orientované, proto se vstupující hrana a vystupující hrany počítají zvlášť. Celkový stupeň uzlu je pak roven součtu vstupujících a vystupujících hran.
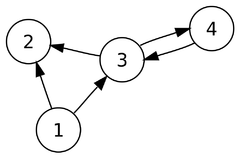
Stupně vrcholů z obrázku vpravo:
| Vrchol | vstupní stupeň | výstupní stupeň |
|---|---|---|
| 1 | 0 | 2 |
| 2 | 2 | 0 |
| 3 | 2 | 2 |
| 4 | 1 | 1 |
Princip sudosti
Tvrzení: V neorientovaném grafu G = (V, E) platí \(\sum_{v\in\mathit{V}}deg(v) = 2\left |E\right |</math>
Důkaz: Je to pouze vyjádření faktu, že každou hranu započítáváme dvakrát - jednou ve vrcholu, kde začíná, podruhé ve vrcholu, kde končí.
Poznámka: Pro orientované grafy změníme levou stranu rovnosti v tvrzení na \(\sum_{v\in\mathit{V}}\left (deg^+(v) + deg^-(v)\right )</math>
Důsledek: Počet vrcholů s lichým stupněm je sudé číslo. Neboli „počet lidí, kteří si na večírku potřásli ruce s lichým počtem účastníků, je sudé číslo“.
Související články
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |