Heavisideova funkce

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)

Verze z 3. 3. 2019, 11:17

H₁(x)

H_1/2(x)

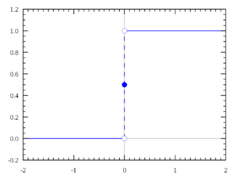
Heavisideova funkce (také jednotkový skok) je nespojitá funkce, jejíž hodnota je nulová pro zápornou hodnotu argumentu a rovna jedné pro kladnou hodnotu argumentu. Hodnota funkce pro nulový argument není podstatná a proto je různými autory definována odlišně (viz níže).

Často se používá v teorii řízení a při zpracování signálu, kde slouží k reprezentaci jednorázové změny signálu. Pojmenována byla po anglickém učenci Oliveru Heavisideovi.

Definice

Heavisidova funkce (s parametrem p) se definuje předpisem:

<math>H_p(x) = \left\{ \begin{matrix} 0 & \mbox{ pro }x<0 \\ p & \mbox{ pro }x=0 \\ 1 & \mbox{ pro }x> 0 \end{matrix}\right.</math>,

kde 0 ≤ p ≤ 1 je reálné číslo určující hodnotu funkce v bodě 0 (platí <math>p = H_p(0)</math>).

Index p je většinou volen pevně a v zápise se vynechává. Heavisidova funkce se potom značí pouze H(x).

Hodnota v nule

Parametr <math>p</math> z definice funkce se nejčastěji volí jako 0, 1/2 nebo 1. Pro hodnotu 1/2 svědčí symetrie výsledné funkce a fakt, že hodnota zpětné transformace Fourierova obrazu funkce v bodech nespojitosti je aritmetický průměr limit zleva a zprava. Důvodem jiné volby může být praktičnost při jistých způsobech použití. V mnoha případech na hodnotě v nule vůbec nezáleží, např. integrujeme-li složený výraz s touto funkcí, neboť Lebesgueova míra množiny <math>\{0\}</math> je nulová.

Nastavíme-li <math>p=H(0)=1/2</math>, můžeme definovat funkci pomocí znaménkové funkce (signum):

Pro případ, kdy <math>p=1</math> nebo <math>p=0</math> můžeme též chápat Heavisideovu funkci takto: <math>H_1 = \chi_{\langle 0, \infty)}</math> respektive <math>H_0 = \chi_{(0, \infty)}</math> kde <math>\chi_M</math> značí charakteristickou funkci množiny <math>M</math>.

Vlastnosti

Mezi jednotkovým skokem a Diracovou funkcí existuje vztah, který lze zapsat jako

<math>H(x) = \int_{-\infty}^x \delta(t)\mathrm{d}t</math>

Derivací Heavisideovy funkce je tedy Diracova delta funkce, primitivní funkcí je tzv. náběhová funkce.

Související články

Externí odkazy

MathWorld, Heaviside Step Function: Mathworld.wolfram.com (anglicky)
MathWorks, Heaviside: Mathworks.com (anglicky)

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii

@@ Řádka 19: / Řádka 19: @@
 Nastavíme-li <math>p=H(0)=1/2</math>, můžeme definovat funkci pomocí znaménkové funkce ([[funkce signum|signum]]):
-: <math>H(x) = \frac{1+\sgn(x)}{2}</math>
+: <math>H(x) = \frac{1+sgn(x)}{2}</math>
 Pro případ, kdy <math>p=1</math> nebo <math>p=0</math> můžeme též chápat Heavisideovu funkci takto: <math>H_1 = \chi_{\langle 0, \infty)}</math> respektive <math>H_0 = \chi_{(0, \infty)}</math> kde <math>\chi_M</math> značí [[Charakteristická funkce|charakteristickou funkci]] množiny <math>M</math>.