V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
Multimediaexpo.cz je již 18 let na českém internetu !!
Tangentová věta
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
m (1 revizi) |
(+ Masivní vylepšení) |
||
| Řádka 1: | Řádka 1: | ||
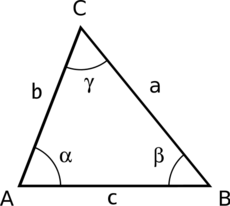
| - | + | [[Soubor:Triangle - angles, vertices, sides.png|thumb|230px|Trojúhelník ABC]] | |
| + | V [[trigonometrie|trigonometrii]] je '''tangentová věta''' tvrzení o rovinných [[trojúhelník|trojúhelnících]]. | ||
| + | Pro každý trojúhelník ABC s vnitřními [[úhel|úhly]] α, β, γ a stranami ''a'', ''b'', ''c'' platí: | ||
| + | :<math>\frac{a-b}{a+b}=\frac{\mathrm{tg}\, \frac{\alpha -\beta }{2}}{\mathrm{tg}\, \frac{\alpha +\beta }{2}}=\frac{\mathrm{tg}\, \frac{\alpha -\beta }{2}}{\mathrm{cotg}\, \frac{\gamma }{2}}</math> | ||
| + | :<math>\frac{b-c}{b+c}=\frac{\mathrm{tg}\, \frac{\beta -\gamma }{2}}{\mathrm{tg}\, \frac{\beta +\gamma }{2}}=\frac{\mathrm{tg}\, \frac{\beta -\gamma }{2}}{\mathrm{cotg}\, \frac{\alpha }{2}}</math> | ||
| + | :<math>\frac{c-a}{c+a}=\frac{\mathrm{tg}\, \frac{\gamma -\alpha }{2}}{\mathrm{tg}\, \frac{\gamma +\alpha }{2}}=\frac{\mathrm{tg}\, \frac{\gamma -\alpha }{2}}{\mathrm{cotg}\, \frac{\beta }{2}}</math> | ||
| + | |||
| + | == Související články == | ||
| + | * [[Tangens]] | ||
| + | * [[Sinová věta]] | ||
| + | * [[Kosinová věta]] | ||
| + | * [[Goniometrie]] | ||
| + | |||
| + | |||
| + | {{Článek z Wikipedie}} | ||
[[Kategorie:Goniometrie]] | [[Kategorie:Goniometrie]] | ||
[[Kategorie:Matematické věty a důkazy]] | [[Kategorie:Matematické věty a důkazy]] | ||
[[Kategorie:Trojúhelník]] | [[Kategorie:Trojúhelník]] | ||
Verze z 5. 9. 2014, 08:26
V trigonometrii je tangentová věta tvrzení o rovinných trojúhelnících.
Pro každý trojúhelník ABC s vnitřními úhly α, β, γ a stranami a, b, c platí:
- <math>\frac{a-b}{a+b}=\frac{\mathrm{tg}\, \frac{\alpha -\beta }{2}}{\mathrm{tg}\, \frac{\alpha +\beta }{2}}=\frac{\mathrm{tg}\, \frac{\alpha -\beta }{2}}{\mathrm{cotg}\, \frac{\gamma }{2}}</math>
- <math>\frac{b-c}{b+c}=\frac{\mathrm{tg}\, \frac{\beta -\gamma }{2}}{\mathrm{tg}\, \frac{\beta +\gamma }{2}}=\frac{\mathrm{tg}\, \frac{\beta -\gamma }{2}}{\mathrm{cotg}\, \frac{\alpha }{2}}</math>
- <math>\frac{c-a}{c+a}=\frac{\mathrm{tg}\, \frac{\gamma -\alpha }{2}}{\mathrm{tg}\, \frac{\gamma +\alpha }{2}}=\frac{\mathrm{tg}\, \frac{\gamma -\alpha }{2}}{\mathrm{cotg}\, \frac{\beta }{2}}</math>
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |